技術資料
正しいインピーダンス測定のための注意事項
本書はBiologic社が発行するApplication note #5を2025年6月において翻訳したものです。今後、原文が改訂され、内容が変更された場合には、改訂後の原文の内容を優先いたします。
1.はじめに
生物細胞の分析、燃料電池の試験、塗膜材の評価、セメントペーストの品質管理など、電気化学インピーダンス分光法(EIS)は電気化学の様々な分野において有効な手法となっています。EISは非破壊かつ高感度な測定手法ですが、正しいデータを得るためには見落とされがちな基本的な注意点があります。本稿は、高インピーダンス系、低インピーダンス系それぞれにおいてEIS測定を用いるときに、セル以外の部分にある誤差要因とその影響を明らかにすることを目的としています。なお、セルに対する一般的な注意点であるサンプルの線形性・因果性・不変性については本稿では言及しないこととします。
EIS測定では、広範囲の周波数にわたって、小振幅の交流電圧または電流信号がセルに印加されます。この範囲の各周波数において、セルの測定インピーダンスは、通常は参照電極(RE)と作用電極(WE)間で収集されるセル電位と、セルに直列に接続された高精度抵抗器の電位降下として測定されるセル電流との複素比で構成されます。当然のことながら、電位および電流測定に影響を与える可能性のあるセル特性、実験パラメータ、電子デバイスの特性、外部要因、または設計上の制限は、EIS実験の精度にも影響を与えます。
2.誤差要因
本稿では、電気化学セルに関連する誤差の3つの基本的な原因、すなわち接続ケーブル、環境ノイズ、そして計測機器の限界について説明します。ほとんどの問題は、ガードされていない長いケーブル、弱い接触、腐食したワニ口クリップなどを用いたケーブル接続に起因します。高インピーダンスのサンプルを扱う電気化学では、ノイズも共通の問題となります。50/60 Hzの電源ピックアップノイズを拾うことはよく起き、セルをファラデーケージ内に置くことで大幅に低減できます。計測機器の限界は、特に電位計の入力に関係します。例えば、電圧測定では、参照電極が電位計の入力インピーダンスに近づくと、分圧の影響を受けやすくなります。良質な参照電極であれば誤差は全く発生しませんが、抵抗率の高い参照電極を使用すると、精度が大幅に低下する可能性があります。
一般的に、非常に高いインピーダンスのセルだけでなく、非常に低いインピーダンスのセルでも、周波数が高くなると問題が発生します。以下のセクションでは、これらのタイプのセルの使用時に発生する具体的な問題に焦点を当てます。
2-1.高インピーダンスなセル
高インピーダンスセルは、主に浮遊容量の存在により誤差が発生しやすくなります。浮遊容量とは、配線に付随する容量を指します。一対の導体の中間に位置する誘電体部品で構成された一般的なコンデンサは浮遊容量とは関係ありません。例えば、配線の浮遊容量は、一方の導体が配線本体で、もう一方の導体がそれ以外の全てのものであり、誘電体は多様な材料に当てはまります。浮遊容量によって、セル電流がグランドへの別の経路を見つけるだけでなく、外部ノイズ源がセルに乱れを与える可能性もあります。
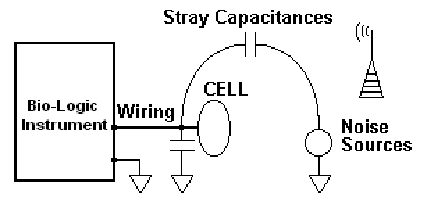
図1. ケーブルに起因する浮遊容量
外部ノイズ源からの影響を低減する簡単な方法は、接地されたファラデーケージを使用することです。物体の電気容量は近傍の物体にも依存しますので、ファラデーケージはグランドに対する浮遊容量を増加させます。これは周波数が大きくなるときに重要な懸案事項となります。
容量性リアクタンスは、周波数が増加するにつれて小さくなり(式(1))、セルからの漏れ電流が大きくなります。そのため、高速な信号の伝達や高周波でのインピーダンス測定の測定確度に影響を及ぼします。

変化の遅い信号や低周波の条件では、浮遊容量の影響はごく微小で無視することができます。ただし、浮遊容量は単純なデジタル電圧計では測定できないことは注意して下さい。
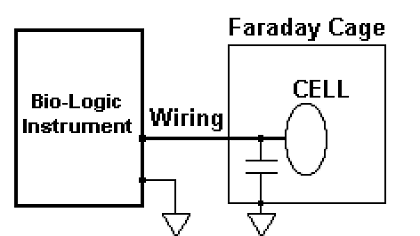
図2. ファラデーケージはノイズを遮断しますが、グランドとの浮遊容量を増幅させます。
例えば、単純な相互ケーブル接続の浮遊容量を評価する方法はあるでしょうか? 電磁気学の法則[1]によれば、まっすぐな円筒形のケーブルの自己インダクタンスと静電容量は次の式で表されます。


ここで、dとhはそれぞれ電線の直径と長さ(メートル)、Lはインダクタンス(µH)、Cはキャパシタンス(pF)です。
例えば、直径1mmのケーブルは、1メートルあたり約1.46µHのインダクタンスと3.12pFのキャパシタンスを示します。これは、理論上、1本の直線ケーブルの場合のものです。しかし実際には、様々な理由から状況ははるかに複雑になります。例えば、接続ケーブルが接地されているか否かに関わらず他の物体の近くに配置されること、ケーブルの先端は単純な直線ケーブルではなくバナナプラグ端子であること、ケーブルの直径と長さは実験上の要件に合わせて変更できることなどです。特定の接続ケーブル長においては、同じ長さの直線ケーブルの場合よりもキャパシタンスが大きくなることが予想されます。実験系の浮遊容量を推定する最良の方法は、空気中(何もつながない状態)、または研究対象の電気化学セルのインピーダンスに近い既知のダミーセル上でインピーダンス測定を行うことです。
浮遊容量がインピーダンス測定に与える影響の例を図3に示します。測定は微小電流測定オプションを装備したVMP3を用い、対極端子と参照極端子(CA1、REF3、REF2)を互いに接続し、作用極端子とセンス電圧端子(CA2とREF1)も互いに接続した2端子で測定しました。
(注:VMP-300 電気化学測定システムの場合、REF1、REF2、REF3、CA1、CA2端子はそれぞれS1、S2、S3、P1、P2端子です。)
微小電流プローブは40 x 20 x 60 cmサイズの接地されたファラデーケージの中心に置きました。インピーダンス測定は電圧制御モードを用いて100 kHzから0.1 Hzまで、0.5 V振幅で以下の3条件において実施しました。
微小電流プローブは40 x 20 x 60 cmサイズの接地されたファラデーケージの中心に置きました。インピーダンス測定は電圧制御モードを用いて100 kHzから0.1 Hzまで、0.5 V振幅で以下の3条件において実施しました。
A-何もつながない
B-長さ10 cm、直径0.5 mmの導線を対極と参照極につないでいる
C-Bと同様の導線で、先端に4 mmバナナ端子をつないでいる
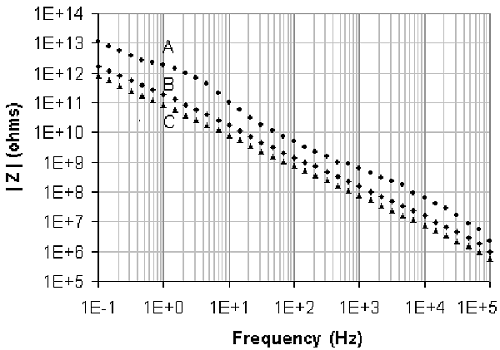
図3. インピーダンスデータ
A:何もつながない、B:10 cmの導線、C:10 cmの導線+4 mmバナナ端子
これら全てのデータは容量性の挙動と一致します。ZFit(EC-Lab®およびEC-Lab Expressソフトウェアで利用可能)などで解析すると、Aのセルがない状態で浮遊容量は0.12 pF、Bの10 cmの導線のみで0.98 pF、Cの導線にバナナ端子がつながった状態で2.1 pFが得られます。セルがついていない状態の0.12 pFの容量(エレクトロメータの入力インピーダンスに対応します)をBの値から引くと、10 cmの導線のキャパシタンスは0.86 pFとわかり、先述の想定の通り理論値より大きくなっています。これはセルの周辺に接地された金属の物質が存在するためです。同様に0.98 pFをCの値から引くと、4 mmバナナ端子が導線に1.12 pFの容量を足していることがわかります。
これは何を意味するのでしょうか?
これらの測定結果は、高周波において、浮遊容量が高インピーダンスサンプルの測定精度に影響を与える可能性があることを単純に示しています。例えば、10kHzを超える周波数では、10cmの配線で10MΩの抵抗を測定した場合、測定インピーダンスは抵抗値ではなく、浮遊容量のリアクタンスに相当します。
2-2.低インピーダンスなセル
ここまで、高インピーダンスなセルに対して高周波領域では浮遊容量を考慮する必要があることを説明してきました。低インピーダンスなサンプルの場合、浮遊容量はサンプルに並列に存在するため考慮する必要はありません。その一方で、サンプルに直列に存在する浮遊インダクタンスが高周波領域で最もありがちな誤差要因となるため、注意深く分析する必要があります。
浮遊容量と同様に、浮遊インダクタンスもケーブルに関係します。式(2)からわかるように、どんな導線にもインダクタンスが存在します。これはサンプルの物理的な形状も例外ではなく、円筒型の電池でのインピーダンス試験でも高周波では誘導性の挙動が見られます。電池を同じ長さの導線に置き換えたときでも、一般的に10 kHz以上の高周波で同様の虚数部分の値が得られます。 誘導性インピーダンスの式を見ると、周波数が大きいほど電流の流れを阻害しようとします。

例えば、長さ10 cm、直径1 mmの導線は約146 nHのインダクタンスを示し、100 kHzの周波数では92 mΩのリアクタンスとなります。
VMP3を用いて10 cmの導線に対して電流制御モードで200 mA振幅のインピーダンス試験を行った結果を図4に示します。サンプルの導線は対極端子に短絡させた参照極端子(CA2、REF3、REF2)と作用極端子(CA2、REF1)の間につながれています。
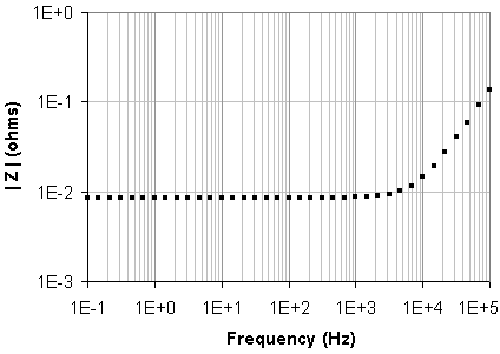
図4. 10 cmの導線に対するインピーダンスの測定結果
このデータは誘導性の挙動を示しています。フィッティング解析を行うと、8.5 mΩの抵抗成分と直列な202 nHのコイル成分があることがわかります。
低インピーダンスサンプルに対しては、導線の自己インダクタンスの他に、変動する磁場の影響もインピーダンス測定の結果を変えてしまいます。
基礎的な電磁気学の法則によると、導線を流れる電流値が変化するとき導線の周辺には変動する磁場が生じ、その磁場はコイル中に起電力を誘起します。(ファラデーの法則)

ここで、ΔBはΔt時間における磁場の変化、Aはコイルの断面積の大きさです。
セルと機器を接続するケーブルには、セル電流を駆動する2本の電流線と、電流が流れない(または非常に小さい)2本の電位検出線があります。電流線を流れる変動セル電流は変動磁場を発生させ、電位検出線に起電圧を誘導します。これは磁気結合効果によるものであり、分析対象サンプルに対して直列に接続された正または負の見かけ上のインダクタンスとして観測されることがあります。

±の極性は磁場がコイルを通過する方向によって決定されます。(図7)
磁気結合効果を理解するために、いくつかの実験を行ってみます。VMP3のケーブルの電流端子(CA1、CA2)と電圧端子(REF1、REF2)をそれぞれショートさせて同じ点につなぎます(図5)。REF3は測定には関係ありませんが、EC-Labソフトウェア上でエラーメッセージが出ないようにグランド端子とつなぐか、REF1、REF2とつなぐようにしています。
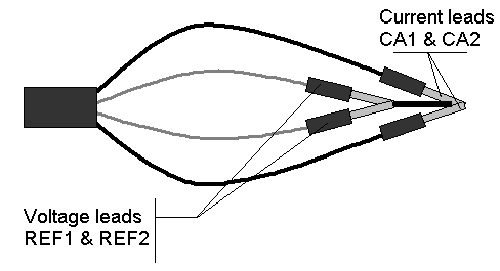
図5. 磁気結合の検証のための接続
測定はVMP3を用いて100 kHzから0.1 Hzまで、1 Aレンジで200 mA振幅により行い、その結果を図6、図7に示します。
これらの結果は磁気結合による誘導性の挙動を示しています。電流線がお互いに遠くなり、電圧端子とも距離を置くような配置、すなわちコイル部分の面積が最大となるように配置したとき、磁気結合による効果が増加しました(図6の「not twisted cables」)。LRの直列回路でフィッティングすると、コイル成分は145 nH、抵抗成分は50 μΩとなります。磁気結合により、高周波領域では±90°の位相差を生じており、先述の通り、極性はコイルを通過する電流の向きによって変わります。
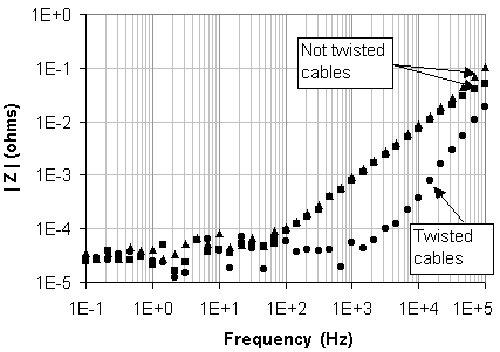
図6. 磁気結合によるインピーダンスの大きさ
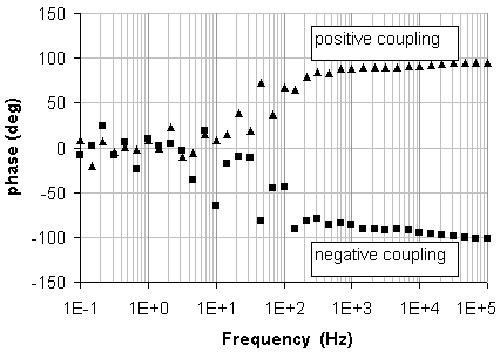
図7. 磁気結合による位相差
電流線をツイストして磁場を打ち消すことと、電圧線をツイストしてコイル領域の面積を小さくすることで磁気結合効果を抑えることができます(図6の「twisted cables」)。ただし、ケーブルをツイストしたとしても、磁気結合により直列に25 nH程度のインダクタンスを生じることがわかります。
外部の変動する磁場によっても電圧線に起電圧が生じることにも注意が必要です。また、一定な磁場でもセルケーブルの振動や単純に動いてしまうことで起電力が生じます。
3.まとめ
一般的に、低インピーダンスまたは高インピーダンスのセルを高周波で測定すると、インピーダンスデータの解釈を誤る可能性が高くなります。測定精度を向上させるには、セルの設計、ケーブル接続、セル環境について特別な注意を払う必要があります。高インピーダンスのセルは浮遊容量の影響を受けやすく、低インピーダンスのセルは浮遊インダクタンスの影響を受けやすいです。
セルを大型のアース付きファラデーケージ内に配置すると、浮遊容量を低減できます。
浮遊容量と浮遊インダクタンスの両方を低減するには、配線を可能な限り短く細くする必要があります。
磁気結合効果は、電流線同士をツイストして磁場を減少させ、電圧線同士をツイストして誘導ループ(コイル状の部分の大きさ)を減少させることで低減できます。
ほとんどの場合、どのようなアプリケーションにおいても、これらの誤差はそれほど重要ではありません。しかし、測定の限界を完全に理解することが、結果を正しく解釈するための鍵となります。限界条件に近い状態で精密な測定を行う場合は、測定誤差の原因となる要因を認識しておく必要があります。測定不確かさを推定する際には、残りの誤差源を考慮する必要があります。
本稿ではインピーダンス測定における一般的な誤差源に焦点を当てていますが、他の電気化学測定法においてもこれらの誤差源を考慮する必要があります。EISとは簡単に言えば、測定セットアップのあらゆる不完全性を「明らかにする」手法であり、高周波化への欲求によって、これらの不完全性が強調されることがしばしばあります。
4. 参考文献
- F. W. Grover, in: Inductance Calculations. Princeton, NJ: Van Nostrand (Ed.), (1946). Reprinted by NY: Dover Publications (1962).
2025年6月翻訳
- Bio-Logic社電気化学測定システム
- ・ハードウェア
- ・EC-Lab
- ・トラブルシューティング
- ソフトウェア
- ・Zviewおよび東陽テクニカ製ソフトウェア
- 電気化学測定
- ・基礎電気化学
- ・インピーダンス
- ・バッテリー
- ・腐食
- ・その他
- 燃料電池
- ・燃料電池評価

















