技術資料
EC-Lab®でのバッテリーと腐食のEIS信頼性評価:THD、NSD、NSR
本内容はBioLogic社が発行するApplication note #64を2025年5月時点で翻訳したものです。今後、原文が改訂され、内容が変更された場合には、改訂後の原文の内容を優先いたします。
1.はじめに
EISは、ある状態の電気化学系の研究において、界面で起こる反応の性質を理解するために使用される有効な測定手法であり、電位または電流の正弦波を印加することで得られる測定系の線形応答解析により求められます。
上記で定義したEISを使用するには、研究対象となる反応系は以下の要件を満たす必要があります。
- 測定系が線形であること
線形な測定系の簡単な例は抵抗です。[1] - 測定系からの応答が一時的ではないこと
定常状態または永続的な状態に達している必要があります。[2] - 測定系を定義するパラメータが実験中不変であること
経時変化する測定系におけるインピーダンス測定は、誤った解釈をもたらす恐れがあります。[3] - 測定系は、実験中一定であること
例えば、不活性化状態から脱不活性化状態に移行する不活性電極は、適切な測定系とは言えません。
ほとんどの電気化学反応は非線形の挙動を示します。しかし、小さな振幅を印加することでそれらの挙動を線形とみなすことができます。この振幅の値は測定系の特性に依存するため、測定系ごとに選択した振幅が十分に小さいことを確認する必要があります。これが、EIS QI™(Quality Indicator)機能の第一の役割、すなわち全高調波歪み(THD:Total Harmonic Distortion)です。
さらに、実験中は測定系とその応答が変化しないようにする必要があります。写真撮影に例えると、シャッターが開いている間は被写体が動いてはいけないのと同じです。そのために、非定常歪み(NSD:Non Stationary Distortion)という2つ目の指標が用意されています。
さらにもう一つ、応答信号の品質に関連したノイズ対信号比(NSR)も利用できるようになっています。これにより、入力信号が小さすぎず、測定されるノイズに比べて応答の振幅が大きくなっていることが確認できます。
このアプリケーションノートでは、まずこれらの指標の計算方法を示し、次にそれらの使用例を示します。
2.理論的説明
この章では、各指標について簡単に説明します。
より理論的な情報については、EC-Lab® User's Manualを参照してください。
2-1.全高調波歪み(THD)
前述したように、電気化学系のほとんどは非線形です。小さな振幅の入力信号を印加することにより、非線形な測定系も線形とみなすことができます。
THDは、測定系に印加される電流振幅、電位振幅のいずれかが線形に振る舞うと見做せるほど十分小さいかどうかを示します。系が非線形に応答する場合、出力信号にはいくつかの高調波が含まれます。THDは、N個の高調波の振幅を評価することによって非線形性を定量化します。
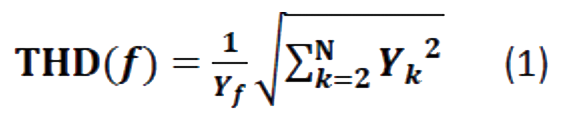
ここで、|Yf| は基本周波数 f(または第1高調波)における信号の振幅、|Yk| はk次高調波の振幅です。
THDはパーセントで表されます。一般的に、5%未満のTHDが許容範囲とされています。EC-Lab®では、THDは電位、電流、および6次高調波(N = 7)に基づいて計算されます。
システムの線形性と非線形性の詳細については、[1]を参照してください。
2-2.非平衡歪み(NSD)
前述のように、測定系とその応答はインピーダンス測定中の経時変化がないことが重要です。
測定系の非定常性には、2つの原因が考えられます。
i)測定系の応答が永続的な状態に達していない。
ii)測定系を定義するパラメータが時間と共に変化している。
非定常な測定系の応答には、基本周波数に加えていくつかの隣接周波数が含まれます。
したがって、NSD指標は以下のように定義されます。
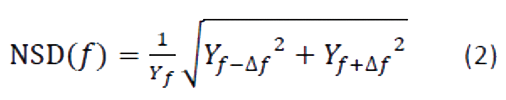
ここで、|Yf| は基本周波数 f (または第1高調波) における信号の振幅、|Yf-Δf| と |Yf+Δf| は基本周波数に隣接するピークの振幅、Δf は周波数分解能 * Δf = 1/T (T は測定の取得時間) です。
NSDはパーセンテージで表現され、電位、電流に基づいて計算されます。 EC-Lab®におけるドリフト補正機能も隣接周波数の補正に基づいています[2]。
2-3.ノイズシグナル比(NSR)
理想的な測定では、すべての信号エネルギーは基本周波数に含まれますが、測定装置の確度や精度、外部からの摂動など、様々な要因により、基本周波数以外の周波数にもエネルギーが含まれる場合があります。これをノイズと呼びます。
NSRは、測定におけるノイズの程度を定量化します。これは次の式で表されます。
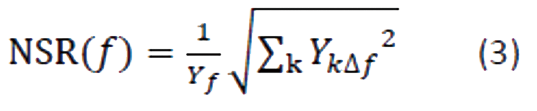
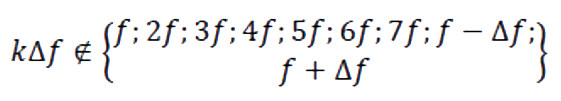
これは、以下に含まれていないすべての信号の寄与を表します。
- 基本周波数
- THDを計算するために使用される6つの高調波
- NSDを計算するために使用される基本周波数に隣接する周波数の信号
これらの指標を説明するためにいくつかの測定結果を示します。
3.電気回路における測定結果
測定はテストボックス3を用いて実施しました。これは、BioLogic社製の電気回路群で、電気化学系の典型的な挙動を模倣しています。最初の回路は線形な系、2番目と3番目の回路は非線形な系で、それぞれターフェルと不動態な系を模倣しています[1]。EIS-QIオプションを有効にするには、EC-Lab®の「詳細設定」に移動する必要があります。
3-1.テストボックス-3#1:線形な測定系
図1のように、テストボックス‐3に対応する電気回路の直流に対する応答は線形です。

図1:テストボックス-3#1の定常状態応答
掃引速度:20mV/s
図2は、振幅を変えながら測定したナイキスト線図を示しています。
これらの測定は、BP-300型ポテンショスタット(現在は販売終了)に微小電流測定用オプションを搭載したチャネルを使用して行いました。
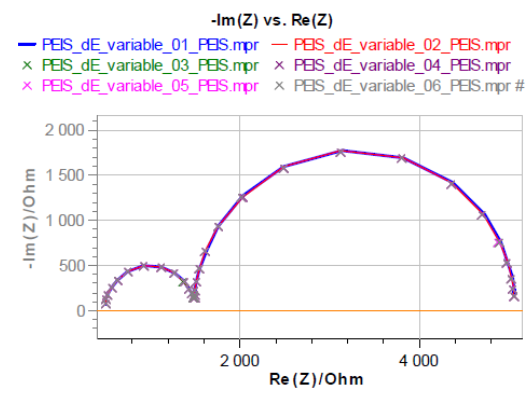
図2:2,5,10,13,15,20 mVと振幅を増加させ、テストボックス-3#1でEIS測定した時のナイキスト線図
周波数範囲:100kHz~1Hz
振幅に関わらず、ナイキスト線図は同じであることがわかります。これらのナイキスト線図は、R1 + R2/C2 + R3/C3の電気等価回路を用いてフィッティングできます。フィッティング結果は表A1に示されています。6回の測定における正規化標準偏差(σ/平均)は0.21%を超えず、インピーダンスは入力振幅に依存しないことを示しています。図3は、6回の測定における電流THD(THD I)を示しています。
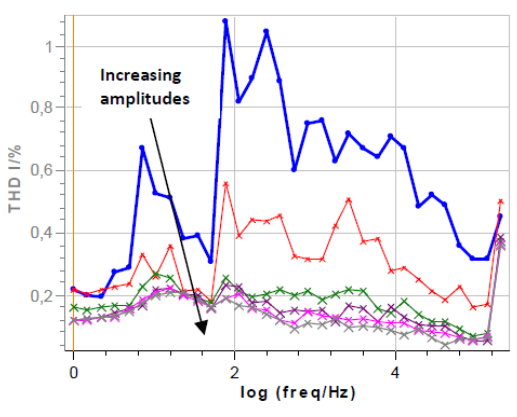
図3:2,5,10,13,15,20 mVと振幅を増加させ、テストボックス-3#1でEIS測定をした時のTHD
周波数範囲:100kHz~1Hz
電流のTHDは1%を超えることはなく、驚くべきことに振幅の増加とともに減少します。これは式1で説明できます。印加電位の振幅が増加すると、基本周波数Yfの振幅も増加しますが、測定ノイズのみに起因する高調波の振幅は同じままです。したがって、THD Iは振幅とともに減少します。
3-2.テストボックス-3#2:非線形な測定系
テストボックス-3#2は、図4に示すようにButler-Volmer 式または Wagner-Traud式を使用した電気化学系を模倣しています。
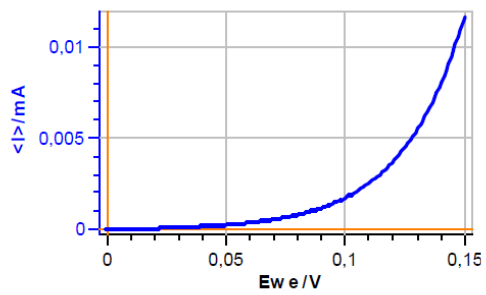
図4:テストボックス3#2の定常状態応答
掃引速度:20mV/s
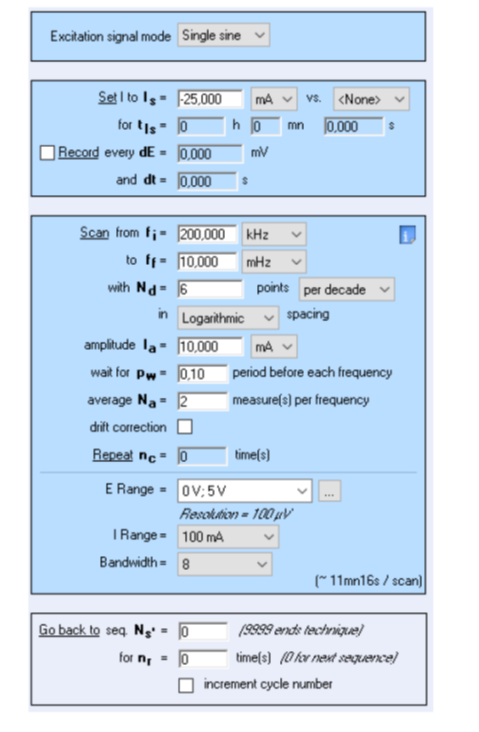
様々な振幅におけるEIS測定を行いました。測定の詳細なパラメータは付録 A1に示します。測定結果を図5に示します。

図5:2,5,10,13,15,20mVと振幅を増加させ、テストボックス-3#2でEIS測定した時のナイキスト線図
周波数範囲:100kHz~1Hz
インピーダンスのナイキスト線図は振幅に応じて変化することがわかります。振幅が増加すると、低周波におけるインピーダンスは減少します。しかし、この回路はR/C電気等価回路を用いてフィッティングすることができます。フィッティングの詳細な結果は付録表AIIに示されています。R1の値の正規化標準偏差は2.34%であり、インピーダンス測定の結果が入力電圧振幅に依存することを示しています。図6は、対応するTHD Iを示しています。
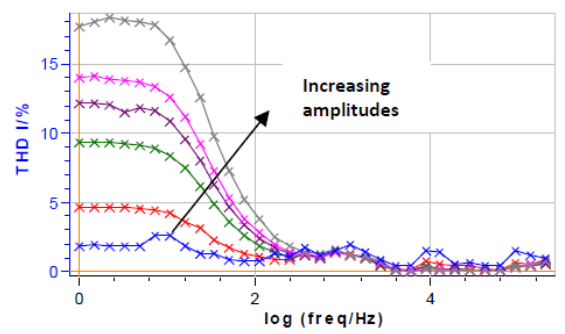
図6:2,5,10,13,15,20mVと振幅を増加させ、テストボックス-3#2でEIS測定した時のTHD I
周波数範囲:100kHz~1Hz
5mVのときTHD Iが5%になり、これは許容範囲内とみなすことができます。5mV以上では振幅が大きすぎて、THD Iが10mVで10%、20mVで約20%になってしまいます。これにより、THD I、ひいては系の非線形挙動も周波数に依存することが分かります。
図6に示す結果より、測定の非線形性を無視する方法があります。それは、測定の周波数を100 Hz(log(100) = 2)以上に制限することで、この値(100Hz)以上ではTHD Iは選択したすべての振幅に対して常に5%以下になります。
この特定の例では、電気回路の構成要素の値が時間の経過と共に変化する理由がないので(温度は実験が行われた部屋で制御されています)、NSDは関係しません。
EC-Lab®で使用可能な最後の指標はNSRです。これはすべての周波数(基本周波数、基本周波数に隣接する周波数および6つの高調波を除く)の振幅を合計し、その合計を応答の基本周波数の振幅で除算した値です。
図7aは、振幅が増加するにつれてNSR Eが減少することを示しています。これは、式3の項Yfが増加していることによるものです。2mVの場合は、THD I(図6)の値からは適切な電圧の大きさであることが分かりますが、 NSR Eの値が大きくなってしまっているため、このインピーダンス測定には不適であることが分かります。5mVの振幅では、NSR Eの値は約5%であり、良好な結果と言えます。
NSR Iの値を考えると、小さな振幅を用いることでノイズに影響を受けやすくなることはさらに明瞭となり、その値は最大で70%にも及びます。
鋸形の信号は電流のオートレンジによって説明されます。低周波になるにつれて電流が減少すると、電流レンジも小さくなります。低い電流レンジに移動すると測定の精度が向上し、測定ノイズとNSR Iが減少します。
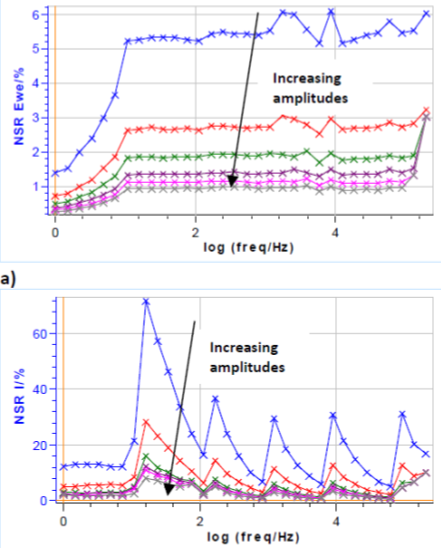
図7:2,5,10,13,15,20mVと振幅を増加させ、テストボックス-3#2でEIS測定した時のa)電位のNSRおよび b)電流のNSR
周波数範囲:100kHz~1Hz
この鋸形のNSR Iは固定の電流レンジを使用することで除去することができますが、これは低周波側で大きな問題となる恐れがあり、測定すべき電流振幅に対して測定レンジが大きすぎることで精度が悪くなり、さらに大きなNSR Iの値となってしまいます。
適切な振幅の選択は非線形性とノイズ信号比との間のトレードオフとなります。図5および図7bからわかるように、高いNSR Iであっても必ずしもノイズの多い測定であると意味するわけではありませんが、10%のTHD Iは測定結果に影響を及ぼす場合があります。
次に、NSD quality indicatorを説明するために非定常な測定系(バッテリーの充放電)に関するいくつかの結果を示します。
4.放電中のバッテリーの測定結果
定電流モードでのインピーダンス測定を、市販のSamsung ICR 18650型バッテリーを用いて実施しました。詳細な条件を付録A3に示します。 放電には2つの異なる放電電流値:-20mA、-25mAを使用しました。
印加した電流振幅は、両方の放電電流に対して10mAです。
図8aは、インピーダンスのナイキスト線図を示し、図8bは電位応答に対するNSDを示します。
応答信号は図8bに示すように、1Hz付近から非定常性によって歪み始め、-20mAの放電電流の場合、NSD Eは15mHzで5%を超えます。放電電流が増加すると、NSD Eは同じ周波数での測定でも増加します。これは、電池の状態が時間とともにより急速に変化するためと考えられます。そのため、このときのNSD Eは50mHzより高い周波数で5%を超えます。
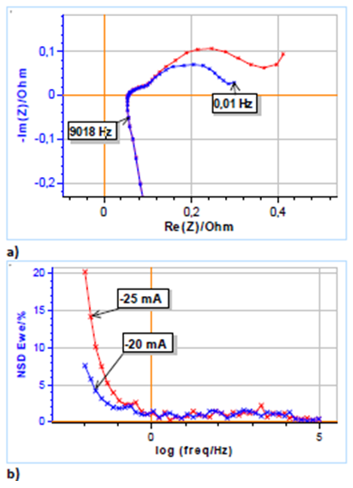
図8:市販の18650 LFPバッテリーa)ナイキスト線図 および b)NSD E 2つの放電電流:-20mA(青色)、-25mA(赤色)。 10mAの変調振幅
周波数範囲:100kHz~10mHz
この場合、NSDは直流によるサンプルの変化に依存するため、非定常性の原因は測定系の変化となります。つまり測定パラメータは同じであってもサンプルの状態が時間とともに変化することです。高周波数では、測定に影響を与えるほど変化が早くありません。
5.まとめ
このノートでは、EC-Lab® 11.20以降で利用可能な3つのパラメータを紹介しました。これらのパラメータは、電気化学インピーダンス測定の信頼性に関する定量的な情報を提供し、最適な入力パラメータの選定に役立ちます。
THDとNSRを使用することで印加するAC振幅を最適化することができ、NSDによって測定系に印加するDCバイアスの大きさを最適化できます。
振幅が小さい場合にはTHD Iが低くなりますが、NSR Eが高くなるため、この妥協点が適切な条件になります。OCP(自然電位)と比較して高い電位を印加した場合、OCVのみを印加した場合よりもNSD Iは確実に高くなります。
これらの周波数依存パラメータは、テストボックス3と市販のバッテリーを用いて得られた測定結果で示されました。
データファイルは以下の場所にあります:
C:\Users\xxx\Documents\EC-Lab\Data\Samples\EIS\AN64_
参考文献
1) Application Note #9 “Linear vs. non linear systems in impedance measurements.”
2) Application Note #17 “Drift correction in electrochemical impedance measurements”
3) Application Note #55. “Interpretation problems of impedance measurements made on time-variant systems.”
付録
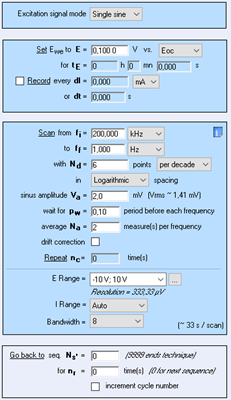
図AI:図2、3、5~7に示す結果のパラメータ。他の振幅も同様
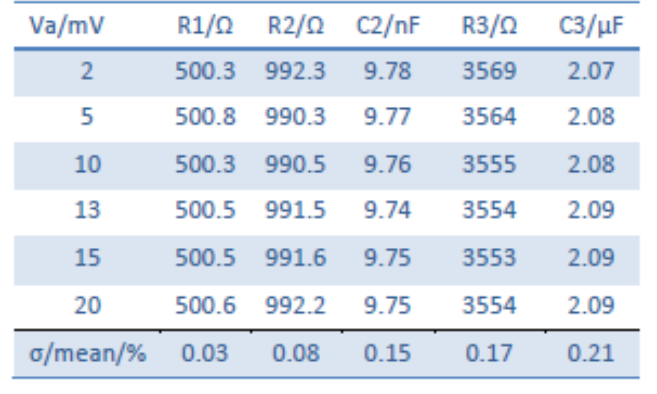
表A1:図2のインピーダンスデータのフィッティング結果
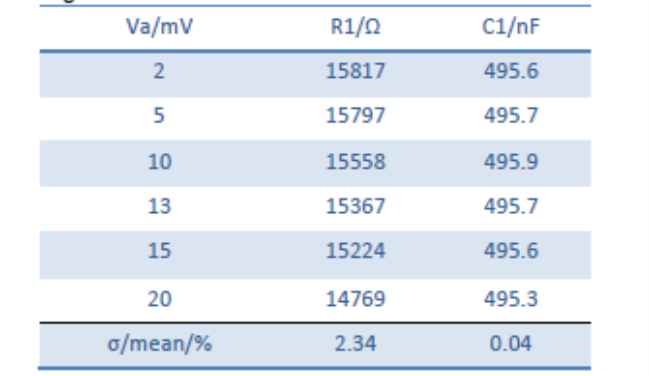
表A2:図5のインピーダンスデータのフィッティング結果
表A3:図8に示す結果のパラメータ
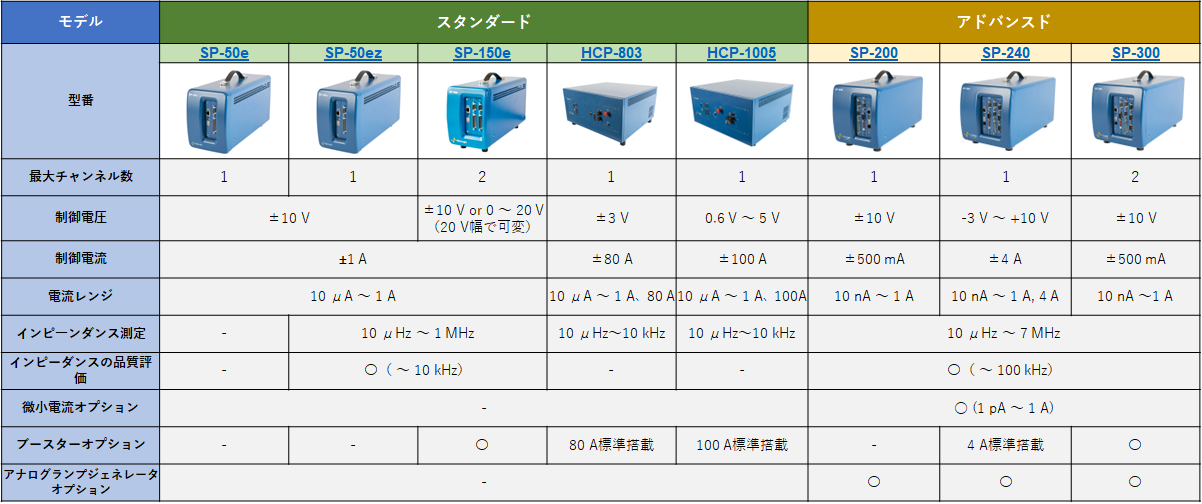
セレクションガイド
Bio-Logic社 シングルチャンネル
※画像をクリックして拡大表示
Bio-Logic社 マルチチャンネル
※画像をクリックして拡大表示
- Bio-Logic社電気化学測定システム
- ・ハードウェア
- ・EC-Lab
- ・トラブルシューティング
- ソフトウェア
- ・Zviewおよび東陽テクニカ製ソフトウェア
- 電気化学測定
- ・基礎電気化学
- ・インピーダンス
- ・バッテリー
- ・腐食
- ・その他
- 燃料電池
- ・燃料電池評価