フラットパンチ圧子インデンテーションによる純チタンの応力-ひずみ解析
はじめに

フラットパンチ圧子画像
チタンは強度・軽さ・耐食性・耐熱性・生体適合性などの様々な優れた側面を持つため、航空機の部品から装飾品、医療機器など幅広く活用されています。その中で、純チタンはチタン合金と比較して加工が容易かつ安価な材料として用いられます。
チタンの強度評価は多くの報告(3)があり、マクロスケールな引張試験機や圧縮試験機を用いた応力-ひずみ曲線による解析が一般的です。近年、ミクロスケールにおいて純チタンはより強度が高くなるという報告(4)もされており、今後も新しい用途への応用が期待されます。
KLA社では特許技術を用いた、フラットパンチ圧子インデンテーションによる微小スケールの応力-ひずみ解析により、ミクロスケールにおける強度評価を実現します 。
理論
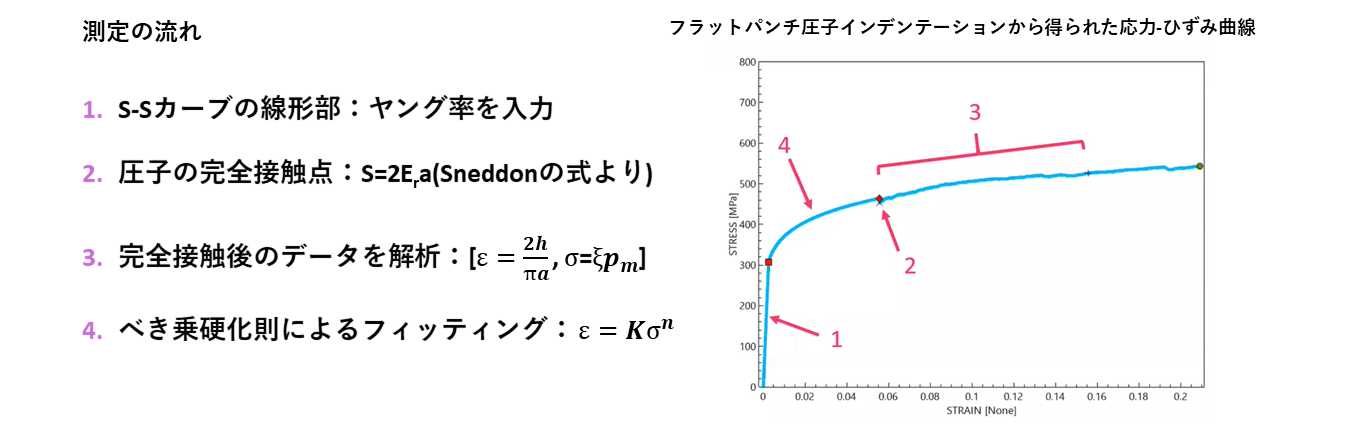
KLA社の特許技術による計算(5)を用いたフラットパンチ圧子インデンテーション試験から、下記の①~④式に基づき応力とひずみの関係を導出します。 まず押し込み深さ h をスケーリング化し、単軸歪み ε に対応するようにします。この時 h と ε の関係はSneddonの式より①式となります。
ε=(2/π)(h/a) ・・・①
次に接触平均圧力 pm についても単軸応力 σ に対応するようにします。この時 pm と σ の関係は➁式の通りです。
σ=ξpm ・・・➁
ここでξは定数ではなく、③式で定義される塑性度のパラメータ S* に依存します。
S*=SL/S ・・・③
SLは負荷曲線の勾配であり、Sは弾性接触剛性になります。完全弾性変形時は荷重勾配SLは接触剛性に等しくなり、完全塑性変形時は除荷勾配が無限大であるため、0<S*<1の値をとります。ここでSを連続的に求めるためダイナミックインデンテーション試験(連続剛性測定方)を活用します。連続剛性測定により③式を用いるための接触剛性は荷重サイクル全体にわたって計算でき、ξはS*を用いると以下④式となります。
ξ=0.39690(S*) + 0.32180 ・・・④
④式の定数は数百種類の材料への有限要素法解析から決定されました。詳細は参考文献(5)をご覧下さい。
実験方法
上記理論に基づいて純チタンの応力-ひずみ曲線解析を実施しました。試験装置は以下の通りです。
フラットパンチ圧子インデンテーションで応力-ひずみ曲線を取得する場合、線系領域は、ヤング率の文献値もしくはナノインデンテーション試験で求めたヤング率を入力します。また上述の理論では応力-ひずみ測定の関係を求める場合、フラットパンチ圧子とサンプル表面が完全に接触する必要があります。完全接触点は試験の過程でSneddonの式に伴う基準時を超えた場合とみなします。この基準点はSneddon(6)の式より、
S>2Ea ・・・➄
となります。この点を超えると応力-ひずみ曲線は式①~④に従って求めることができます。完全接触点を超えたこれらの応力-ひずみ曲線から、加工硬化指数 n を得るためのべき乗硬化則でのフィッティングを可能にします。
σ=Kεn ・・・⑥
ここから完全接触前の応力-ひずみ曲線を①式および⑥式に従って、求めることができます。降伏点は⑥式と、入力したヤング率により設定される応力-ひずみ曲線の線形部分との交点として報告しています。
結果
12点インデンテーション試験を行った箇所をFigure.1に示します。12点の試験における降伏点は270±50MPaとなり、この値はメーカーが報告している値(2)240MPaとよく一致していることがわかります。またその他の論文で報告されている値(3)の範囲内であることもわかります。
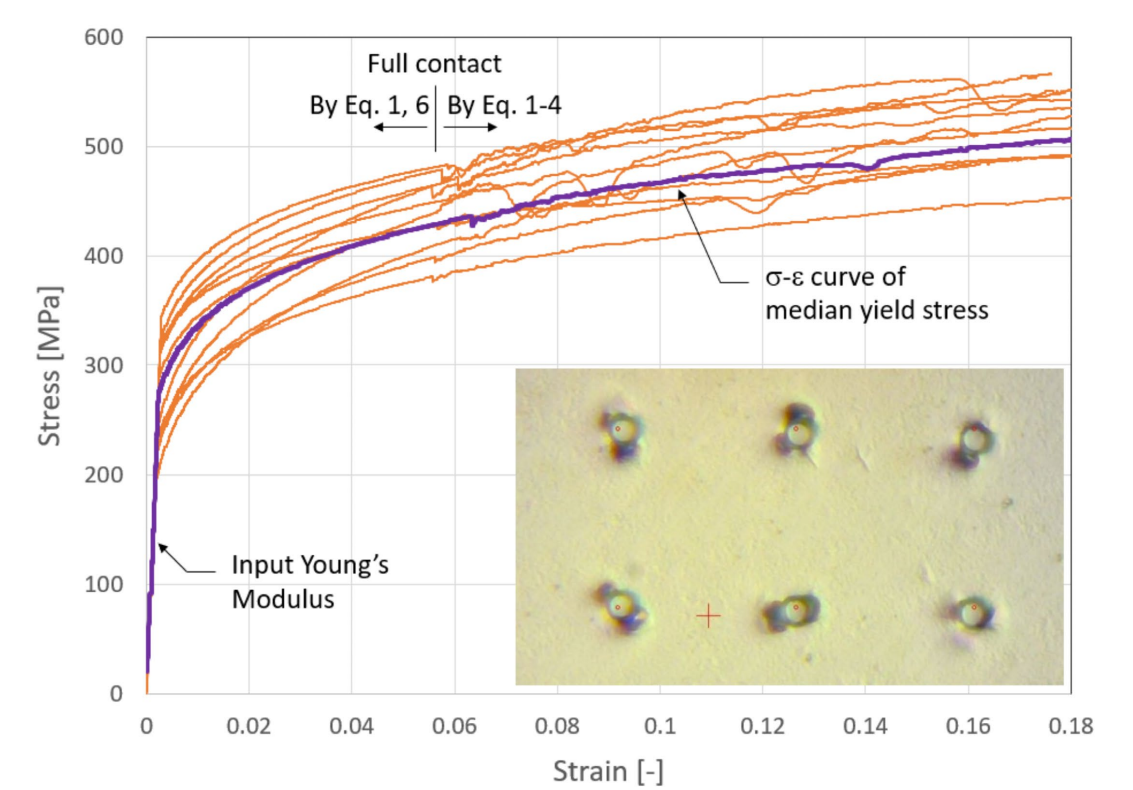
Figure.1 フラットパンチ圧子インデンテーションの測定結果
以前から球径圧子を用いたインデンテーションによる微小域での応力-ひずみ曲線の測定(7)は行われていますが、残念ながら限られた結果しか得られていません。球形圧子の接触面積の不確かさや、接触面積が増えると、試験サンプルのボリュームも徐々に同時に増えていくため、サンプルボリュームとひずみの両方が同時に変化するためです。
一方でフラットパンチ圧子は接触面積が既知であるため、試験を通して一定であり、サンプルボリュームも試験を通してほぼ一定となるため、応力-ひずみ曲線の評価に適しています。
関連製品
参考文献
- H. Tada, “Manufacturing technologies for titanium eyeglass frames,” Titanium for Consumer Applications, Chapter 13, editors F. Froes, M. Qian, M. Niinomi, Elsevier, 2019: 235-268.
- Kyocera, Titanium Properties, https://kyocera-sgstool.co.uk/titaniumresources/titanium-information-everything-you-need-to-know/titaniumproperties/, accessed March 9, 2020.
- R. Osman and M. Swain, “A Critical Review of Dental Implant Materials with an Emphasis on Titanium versus Zirconia,”Materials (Basel) 2015: 8:932-958.
- W. D. Nix and H. Gao, “Indentation size effects in crystalline materials: A law for strain gradient plasticity,” Journal of the Mechanics and Physics of Solids, 1998; 46(3):411-425.
- J. Hay, “Instrumented indentation apparatus having indenter punch with flat end surface and instrumented indentation method using the same,” US Patent US10288540B1, KLA Corporation, 2019.
- I. N. Sneddon, “The relation between load and penetration in the axisymmetric Boussinesq problem for a punch of arbitrary profile, “ International Journal of Engineering Science, 1965.
- E.G. Herbert, G.M. Pharr, W.C. Oliver, J.L. Hay and B.N. Lucas, “On the measurement of stress-strain curves by spherical indentation,” Thin Solid Films, 2001.
この記事は下記の論文の要点を抜き出したものです。さらに詳細をお知りになりたい方は下記の論文をご参考ください。
Microscopic Measurement of the Stress-Strain Relation for Commercially Pure Titanium