技術資料
回転電極法を用いた拡散係数の導出
I. はじめに
回転電極(Rotating Disk Electrode, RDE)は、電気化学測定において拡散係数や反応速度定数を求めるための重要なツールです。 本章では、Bio-Logic社製BluRev RDEシステムを用いて、電気化学インピーダンス測定(EIS)を通じた拡散係数の導出方法について解説します。
II. 実験概要
■II.1. 測定対象
本実験では、0.1 M KCl中に5 mMのK₃Fe(CN)₆およびK₄Fe(CN)₆を含む溶液を用います。この系では以下の酸化還元反応が進行します:
[Fe(CN)₆]³⁻ + e⁻ ↔ [Fe(CN)₆]⁴⁻
両成分が等モル濃度で存在することで、電極の平衡電位が安定し、拡散係数の測定に適した条件が整います。
■II.2. 実験装置
<p>本実験では、Bio-Logic社製 BluRev RDEシステム(図1)を使用し、ポテンショスタットにはBio-Logic社製 電気化学測定装置(スタンダードモデル)を用います。BluRevは、モータと回転シャフトで構成され、先端に電極チップを装着可能です。電極には、直径2 mmのPtディスク電極(型番: 094-Pt/2)を使用しました。
図1. Bio-Logic社製BluRev RDEシステム
■II.3. インピーダンス測定の設定
Bio-Logic社製電気化学測定システムに付属の測定解析ソフトウェアEC-Labを用いて設定を実施しました。
- PEIS -> WAIT -> LOOP(回転数の手動制御)

- PEIS -> RDEC -> LOOP(回転数の自動制御)

インピーダンス測定(EIS)は、以下のプロトコルを用いて実施しました(図2)。

図2. EC-Lab上での設定
III. 各回転数における結果
図3に示すように、高周波領域の応答は電荷移動抵抗(すなわち酸化還元反応に伴う電子移動に関連する抵抗)に対応しており、回転速度による変化は見られません。 一方、低周波領域では、回転速度0 rpmの条件下で半無限拡散挙動を示しますが、回転速度の増加に伴い、実数部の低周波数限界が減少します。

図3. 各回転数での測定結果
IV. 解析
■IV.1. 静止状態(0 rpm)における解析
Randles回路(図4)を用いて解析を行い、ワールブルグインピーダンスを利用して拡散係数を導出しました。ワールブルグ要素σの値を用い、式(1)により拡散係数Dを7.13 × 10⁻⁶ cm²と算出し、文献値と一致しました。
𝐷X=2(𝑅T/(𝑛2𝐹2C*𝜎A ))2 (1)

図4. 静止系における等価回路
■IV.2. 回転電極(1000-5000 rpm)における解析
回転電極を用いた測定では、拡散と対流の両方が関与するため、従来のワールブルグインピーダンスではなく、EC-Labソフトウェア内のZ-Fit解析機能で利用できるWδとWinfの2つの要素を用いてフィッティングを行いました(図5)。Wδ要素は有限拡散要素を表し、ネルンストモデル近似に基づいています。このモデルでは、電気化学反応による物質の濃度変化が拡散層内に限定され、拡散層外側(バルク層)では濃度が一定とみなされます。一方、Winf要素は、ディスク電極における拡散/対流の解析的記述の数値近似に基づいています。そのモデルは、電極の近くの限られた領域にとどまらず、電解質全体にわたる濃度変化を考慮した、より実際の状況に即したモデルです。

図5. 回転系における等価回路
IV.2.1. Wδ要素を用いた拡散係数の導出
インピーダンス測定結果に対してWδ要素を用いたフィッティングを行うことで、時定数𝜏dが得ることができます。回転速度Ω(rpm)、動粘性係数ν(cm² s⁻¹)、定数𝑘L(=1.611)と合わせて以下式(2)へ入力し、測定対象の拡散係数を算出できます。
𝜏d = 𝑘L2𝐷X-1/3𝜈1/3Ω-1 (2)
その際、単一回転数の結果を用いて拡散係数を求められることも可能ですが、回転数の逆数を横軸に、時定数𝜏d を縦軸にしたプロットし、その傾き𝑘L2𝐷X-1/3𝜈1/3から拡散係数を算出する方法のほうが信頼性の高いデータを取得できます。図6に示すように、回転数ごとにフィッティングから得られた𝜏dをプロットし、直線の勾配から算出した拡散係数は7.01 × 10⁻⁶ cm² になりました。

図6. 2000rpmにおけるWδ要素を用いたフィッティング結果
IV.2.2. Winf要素を用いた拡散係数の導出
Winf要素を用いた解析では、回転速度Ωおよび動粘性係数νを入力することで、EC-Labソフトウェア上で測定対象の拡散係数を直接導出することができます。また、複数の回転速度で得られた拡散係数の平均を算出することで、より信頼性の高いデータを得ることができます。異なる回転数によって測定で得られた拡散係数(表1)の平均値は8.00 × 10⁻⁶ cm²/s となり、前述の2つの解析方法で得られた値よりも大きな結果となりました。
図7. 2000rpmにおけるWinf要素を用いたフィッティング結果
*参考として2000rpmのデータを図7に示します。
表1. Winf要素を用いて各回転数で直接算出した拡散係数の結果

V. 考察
前述の通り、Winfによるフィッティングでは、電極の回転速度と電解質の動粘度が分かれば、拡散係数を直接算出することができます。他方、静止電極におけるワールブルグ要素を用いて拡散係数を求めるには、物質の濃度と反応面積の情報が必要となります。 また、EIS測定結果の解析を行うことで、各要素の妥当性を比較できます。例えば、実験値とフィッティング曲線の残差を比較することでモデルの妥当性を定性的に評価できます。EC-Lab上で残差プロットを表示し確認した結果、Wδ要素を用いた場合ではRe(Z)とIm(Z)の残差はそれぞれ±1.5%と+15/-5%の範囲内に分布していたのに対し、Winf 要素を用いた場合では、 それぞれ ±0.4% および +2.5/-1% の範囲内に収まり、Winf の方がより妥当なモデルであることが確認できました。
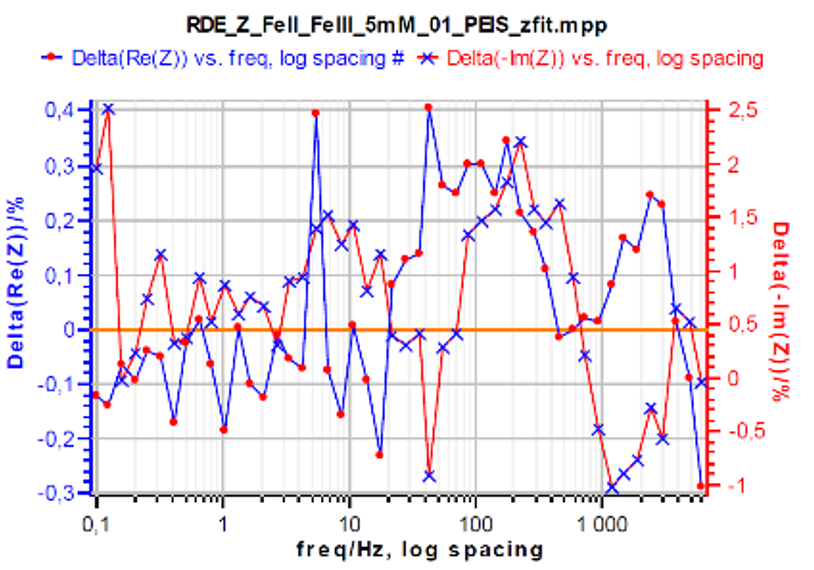
図8. WinfとWinfをそれぞれ用いてフィッティングした際の残差の比較
VI. まとめ
本文書では、Bio-Logic社製BluRev RDEシステムを用いた拡散係数の測定方法を説明しました。Bio-Logic社製電気化学測定システムに付属するソフトウェアEC-Labの分析モジュールであるWinf要素を利用することで、反応面積及び物質濃度の情報がなくとも、より正確な拡散係数を追加計算なく直接算出することができます。
VII. モデル式に関する補足
■VII.1. 静止電極における溶解した電気活性種の濃度インピーダンス表現

■VII.2. ネルンスト近似を用いた回転電極における溶解した電気活性種の濃度インピーダンスの表現

■VII.3. 解析的近似を用いた回転電極における溶解した電気活性種の濃度インピーダンスの表現
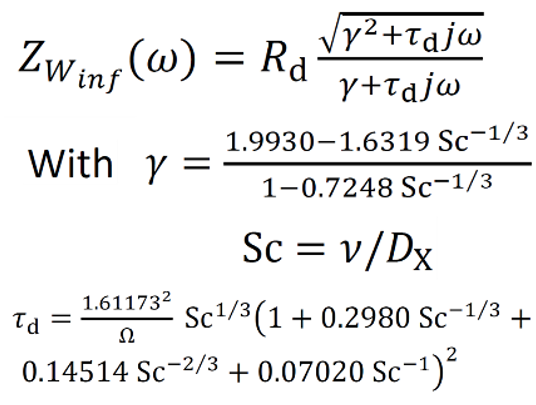
参考文献
本稿はBio-Logic社の以下の文書を編集して作成しました。
EIS measurements on a RDE Part I: Determination of a diffusion coefficient using the new element Winf Electrochemistry – Application Note 66
- Bio-Logic社電気化学測定システム
- ・ハードウェア
- ・EC-Lab
- ・トラブルシューティング
- ソフトウェア
- ・Zviewおよび東陽テクニカ製ソフトウェア
- 電気化学測定
- ・基礎電気化学
- ・インピーダンス
- ・バッテリー
- ・腐食
- ・その他
- 燃料電池
- ・燃料電池評価






