スピーカ計測・評価技術 / 第3回
大信号時のスピーカ特性
スピーカユニットは、小信号で駆動しているときと大信号で駆動しているときでは、その性質が異なります。小信号時=ボイスコイルの変位が小さい時は線形であるのに対し、大信号時=ボイスコイルの変位が大きい時は非線形性を持ち、ひずみの原因となります。どの程度の電圧/音量で大信号、つまり非線形領域での駆動となるかは、そのスピーカユニットのサイズや重さ、形状で決まります。
線形駆動時の特性は、第1回のT/Sパラメータで解説いたしました。今回は、大信号時の非線形の性質をどのように定量化し評価していくか、解説していきます。
T/Sパラメータにおいては、Re、fs、ZL(f)、Bl、Kms、Mms、Q値等が一意に決まりました。しかし、一意に決まるのは、ボイスコイルの位置、つまり変位振幅が小さい時(スピーカユニットの大きさに対して)に限られ、変位振幅が大きい時は一意にT/Sパラメータは定まりません。特にBlやKms、インダクタンスは変位に応じて大きく変化します。それらはボイスコイルの振幅を入力信号と異なるものにし、ひずみとなって音が伝播していきます。そのため、変位振幅が大きい時、つまり非線形時の諸特性の把握は、スピーカの音質向上には不可欠です。それだけでなく、非線形時の特性を評価する利点には以下が挙げられます。
- 音圧出力(特に低周波領域)の限界の把握
- 過負荷による欠陥発生、破壊の防止
- ボイスコイルのオフセットに伴う不安定性の把握
- 設計最適化による小型化、コスト削減
- 効率向上による省消費電力化
- ボイスコイル変位に基づくスピーカの自己保護の実現
昨今では、スピーカ製品の小型化やポータブル化(軽量化)、バッテリ駆動に伴う省電力化が求められています。それらの市場要求を実現するために、非線形特性を把握することは重要となるわけです。では、代表的な非線形性について、解説していきます。
スティフネスの非線形性:Kms(x)
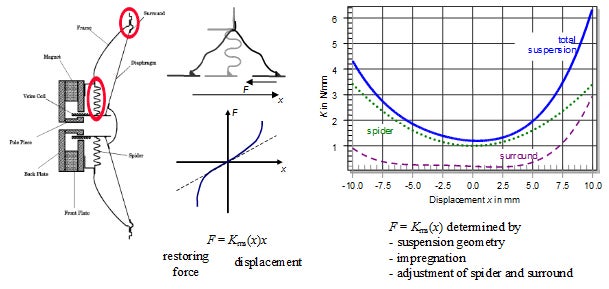
図1.スティフネスKms(x)の非線形性
スピーカのスパイダーとエッジ(図1内左側の赤丸)がバネとなり、ローレンツ力により駆動したボイスコイルを、元の位置に戻します。その関係は、F=Kms(x)xで表されます。ボイスコイルの変位が小さいうちはスティフネスKms(x)の変化はほとんどありませんが、変位が大きくなると、スパイダーとエッジのコルゲーション(溝がいくつも連なっていることで伸び縮できる形状)が伸びます。さらに、コルゲーションが伸びることでそれ以上伸びることができなくなり、結果としてスティフネスが大きくなる=硬くなっていきます。伸び具合は変位によって異なりますので、変位に応じたスティフネスを持つことになります。それを表すために、横軸に変位、縦軸にスティフネスをとったのが図1の右側にあるグラフです。スティフネスの大きい領域で駆動しているとき、駆動力に対する変位が低下します。つまり波形が歪み、ひずみが生じてしまいます。
力係数の非線形性:Bl(x)
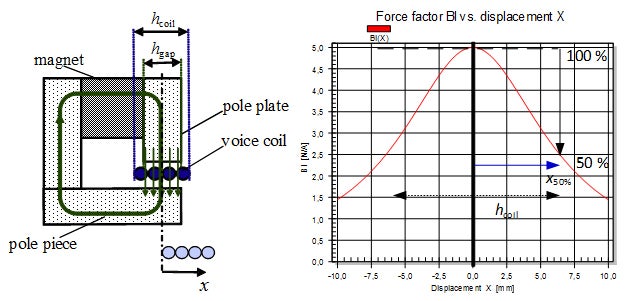
図2.力係数Bl(x)の非線形性
力係数Bl(x)は、ダイナミック型スピーカにおける電気的な領域(音源をボイスコイルに印加するところ)と機械的な領域(ボイスコイルを振動させるところ)を結ぶ重要なパラメータです。この性質はスピーカユニット内部の磁束密度Bとボイスコイル巻線幅l、ボイスコイル変位xで決まります。ボイスコイルの位置が図2のPole plateの直下にあるとき、ボイスコイルの巻線は多くの磁界を得ることができます。つまり力係数Bl(x)は大きくなり、十分な駆動力を生みます。一方、ボイスコイルがPole plateから離れた位置にある場合、つまりボイスコイル変位が大きい時、ボイスコイルの巻線はPole plateとPole piece間の磁界から外れます。そうすると磁束密度Bが小さくなりますので、力係数Bl(x)は小さくなり、駆動力が得られません。横軸をボイスコイル変位x、縦軸をBl(x)としてグラフにプロットしたものが、図2の右側の図です。ボイスコイル変位が大きいと力係数が小さくなりますので、ボイスコイルが十分な駆動力を得られず、信号波形を正確に再現できなくなります。つまり、ひずみが生じてしまいます。
これを解決するためにボイスコイル巻線幅を長くするという手があります。そうしますと、図3のようになります。
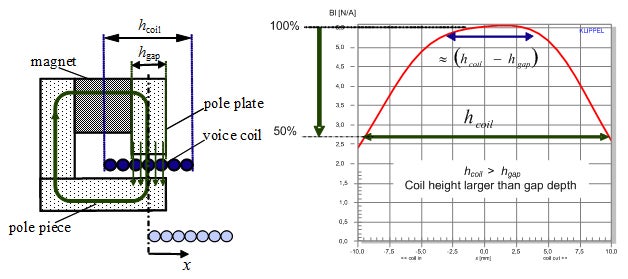
図3.ボイスコイル巻線幅が長い時の力係数Bl(x)の非線形性
これは、低音用のスピーカであるウーファーの伝達関数で、振動系の共振周波数fsを100Hz以下(上図では50Hz)にもっています。この共振周波数をピークに12dB/オクターブ(周波数が2倍になるごとに12dB=0.25倍)変位が減少します。しかし、スピーカ表面の分割振動によって単調な現象とはならず、いくつかのピークを持つことになります。分割振動については、後に解説いたします。
こうすることで、ボイスコイル変位に対し、Bl(x)が一定となる領域が大きくなります。これにより線形駆動領域が増えますので、ひずみを低減することができます。その他にも、各部材の長さや厚みを調整することでも同様の効果が得られます。しかし、いずれの対策であってもスピーカユニット全体を大きくしなくてはならず、コストを増加させてしまいます。できる限りBl(x)に起因するひずみが少なくするためには、スピーカユニットあたりのコストや形状の制約を考慮した上で、Bl(x)を最適化する必要があります。
ボイスコイルのインダクタンス:Le(x, i=0)
ボイスコイルでは、当然ですが、コイルに電流が流れていますので、それに応じた交流磁場を発生することなります。それは、交流抵抗つまりインダクタンスとして作用します。これ前記2つと同様に非線形性を持ちます。
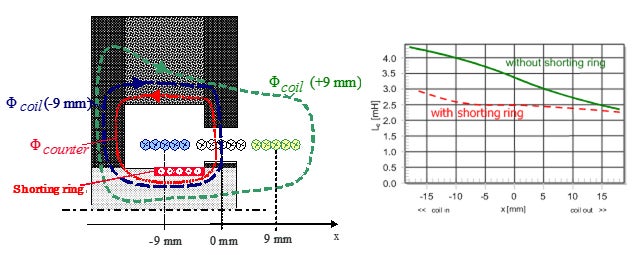
図4.ボイスコイルのインダクタンスの非線形性とその解決策:ショートリング
例えばボイスコイルがスピーカユニットの外側にあるとき(図4左側 緑色のコイル)は、インダクタンスは低下します。一方、内側にあるとき(図4左側 水色のコイル)は周辺を金属に囲まれていることから、インダクタンスは大きくなります。横軸に変位x、縦軸にインダクタンスLeをとったグラフが図4の右図です。このように非対称性を持つようになります。
インダクタンスは周波数が高くなれば増加する傾向にありますので、低周波数領域にはあまり影響を及ぼしません。また、高周波数領域では変位が小さいため、一見、Le(x, i=0)はあまり影響を及ぼさないように見えますが、実は違います。音楽信号のようにベース音やバスドラム等の楽器音にボーカルが乗っている場合、変位が大きいにもかかわらず、高周波領域の音も発生しています。このような場合、インダクタンスの影響でひずみが発生します。これは相互変調ひずみとして観測することが効果的です。なお、ひずみの分類については、後の記事にて解説いたします。
この解決策としては“ショートリング”が有効です。図4の左図内、赤で色が塗られた部分がそれにあたります。ショートリングによってボイスコイルにより発生する磁場と反対方向の磁場が発生することで、ボイスコイルがユニットの内側にあるときのインダクタンスを低下させます。
なお、本項では電流i=0として考えましたが、電流の大きさに対しても非線形性を持ちます。詳細は本記事では割愛いたします。
非線形性を考慮したの等価回路
これまで開設した非線形性を加味した等価回路を図5に示します。
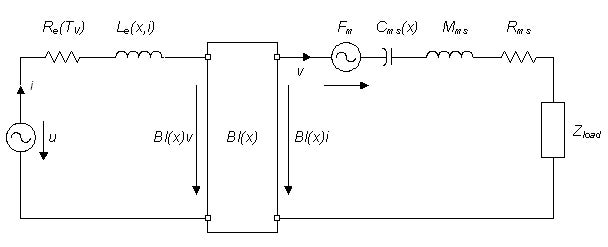
図5.非線形性を考慮した等価回路
左側の電気的な領域においては、インダクタンスLe(x, i)とボイスコイルが動くことによる逆起電力Bl(x)vが、機械的な領域では駆動力Bl(x)iとインダクタンスLe(x, i)が影響する磁気抵抗Fm、サスペンションのコンプライアンスCms(x)=1/Kms(x)が非線形性を持ちます。代表的なものはここまでになりますが、スピーカの仕様によっては他の非線形性も考慮する必要が出てくる場合があります。(ご興味のある方はぜひお問い合わせください)
非線形性の測定方法
これまで解説してきました非線形性の測定には静的な方法と動的な方法があります。静的な方法は従来から行われてきた方法で、DC信号を用います。手軽な方法ではありますが、測定点数を多くする場合は時間がかかる、粘弾性特性に伴うクリープ効果やヒステリシスの影響を受ける、DC信号をもちいているために逆起電力を得られず、インダクタンスの非線形性の評価が安定しない、等の欠点があります。 一方、近年広く行われているのが動的な方法です。
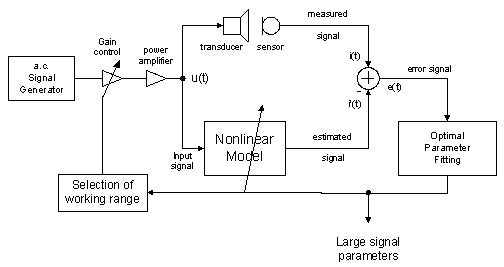
図6.非線形性を測定するための動的な方法
動的な方法では、DC信号の含まれない、音楽信号に近いランダムノイズを十分な振幅で印加し、非線形性を測定します。
まず、図6の一番右側にある“Signal Generator”より、測定用信号が出力されます。これに対し、スピーカユニットを保護するためのリミッタの役割を担う“Gain Control”と信号増幅用の“Power amplifier”を介して、測定対象となるスピーカユニットに信号“u(t)”が印加されます。一方、KLIPPELでは独自技術による非線形のスピーカモデル(図6内の“Nonlinear Model”)に対しても、信号“u(t)”の情報を与えます。
測定対象のスピーカユニットでは、電流、電圧、変位を測定し各種非線形パラメータを算出します。実際の測定データより算出された非線形パラメータとモデルにより算出された非線形パラメータを比較して、その誤差e(t)が最小となるようにNonlinear Modelを改善していきます。その結果、精度の高い非線形パラメータを算出することができるのです。最初にでできたリミッタであるGain Controlは非線形パラメータにより設定されます。つまり、Bl(x)やKms(x)、インピーダンスから算出されるボイスコイルの温度変化でリミットをかけることができることで、ドライバの破壊を防ぎながら、より広い非線形領域までの測定が行えるようになります。
次回は、スピーカから発生する“ひずみ”について、解説していきます。
- 第6回 スピーカ特性シミュレーションとモデルベース聴感試験
- 第5回 ビリつき音(Rub&Buzz)
- 第4回 スピーカから発生するひずみ
- 第3回 大信号時のスピーカ特性
- 第2回 スピーカの表面振動と音の伝播
- 第1回 スピーカユニットの性能評価:TSパラメータ