技術資料
電気二重層の静電容量測定
I- はじめに
電気化学的過程はすべて、電極/電解液の界面、すなわち電気二重層(図1)で発生します。Helmholtz、Gouy-Chapman、Stern、およびGrahameなどにより、この層のさまざまなモデルが提唱されています[1,2]。
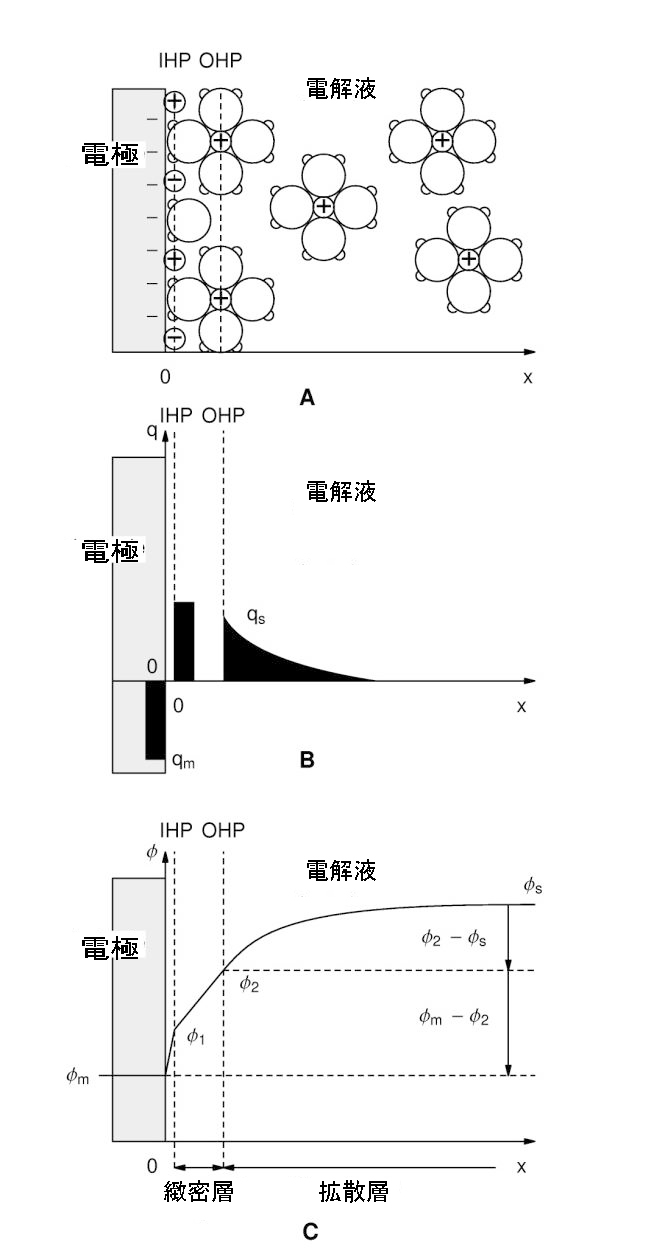
図1:Grahameモデルに従う電気二重層の様子(出典:〔2〕)
IHP:内部ヘルムホルツ面、OHP:外部ヘルムホルツ面
A:負電荷過剰の電極、B:電荷の局在化、C:電極/電解液の界面に対する電位の変化と距離の関係
二重層の構造は、1つの誘電体によって分けられた2つの電極から構成されるキャパシタに類似しています。誘電体の厚みは、イオン半径、つまり50nmに相当します。
本項では、酸性条件における鉄電極の電気二重層について説明します。またその解析手法として、電気化学的インピーダンス分光法(EIS)およびサイクリック・ボルタンメトリ(CV)という2つの手法を使用して、静電容量の値を測定する方法を説明します。
Ⅱ- 実験条件
測定は、EC-Lab®ソフトウェアによって制御されるVSP電気化学測定システムを用いて、HCl溶液(0.1M)を電解液として行います。
以下の3つの電極をセットアップして使用します。
- 作用電極:表面積が3.14mm2の鉄製の回転ディスク電極(RDE)
- 対極:プラチナ線
- 参照電極:飽和カロメル電極(SCE)
実験は電極の回転速度ω= 800rpm(回転/分)で実行します。
CVにおける掃印速度は40mV.s-1です。
どちらの手法の場合でも、データ分析はEC-Lab®ソフトウェアによっても計算できます。
Ⅲ- インピーダンスの考え方
図2で示す等価回路は、並列のキャパシタと抵抗、それに溶液抵抗に対応する抵抗を1つ直列に接続しており、電気二重層を模擬したモデルです。
この場合、得られるナイキスト線図は、完全な半円に近い形になります(図2)。
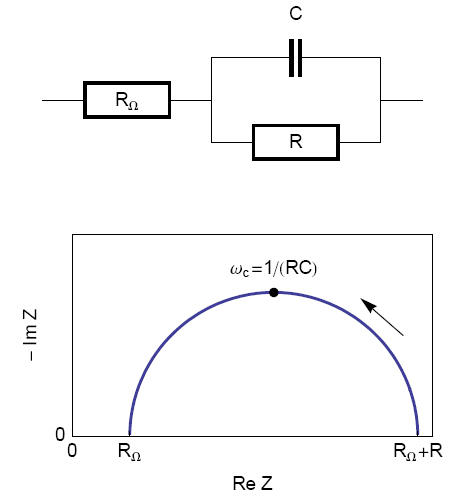
図2: 等価回路RΩ+R/C(上)に対応するナイキスト線図(矢印は角周波数の増加方向を示す)
ただし、実際の実験系において、このようなことはほとんどありません。そのため、コンスタント・フェーズ・エレメント(CPE)(図3ではQとして表記)を導入し、R1+Q/R2の等価回路で静電容量Cの代わりに使用します[3,4]。このとき、得られるナイキスト線図(図3)は、上部が押しつぶされたような半円形になります。
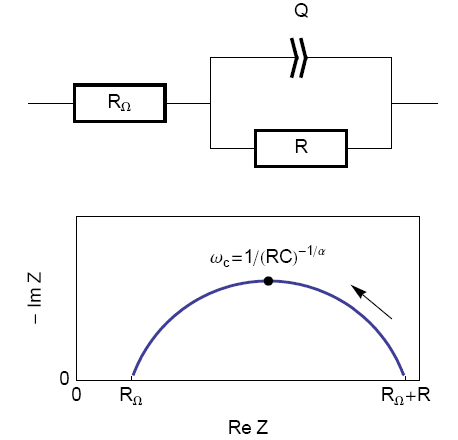
図3: 等価な電気回路RΩ+R/C(上)に対応するナイキスト線図(矢印は角周波数の増加方向を示す)
図2と図3の関係から式(1)が得られ、この式からナイキスト線図の頂点に対応する周波数での静電容量の値が得られます。
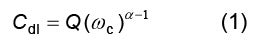
二重層の構造は、1つの誘電体によって分けられた2つの帯電領域から構成される蓄電器に類似しています。誘電体厚は、イオン半径、つまり50nmに相当します。
本書では、酸性条件における鉄製電極の電気二重層について説明します。その目的のため、電気化学的インピーダンス分光法(EIS)およびサイクリック・ボルタンメトリ(CV)という2つの手法を使用して、静電容量の値を特定します。
IV- インピーダンス測定の結果と分析
測定は、電圧制御によるインピーダンス法(PEIS)を使用し、開回路電圧Eocにおいて周波数範囲100kHz~100mHz、振幅(Va)10mVで実行されます。
インピーダンス測定の設定値を図4に示します。
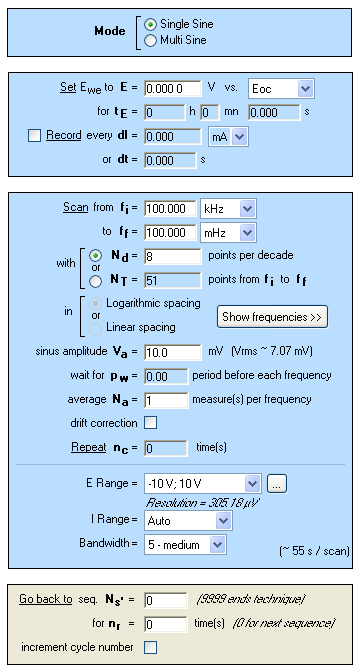
図4:インピーダンス測定のパラメータ設定
図5の低周波数領域(Re(Z) ≥ 55kΩ)の点を見ると、非定常状態であるため、実験系が時間の経過に伴って変化していることが明確にわかります。そのため、それらの点は解析の範囲外とします。
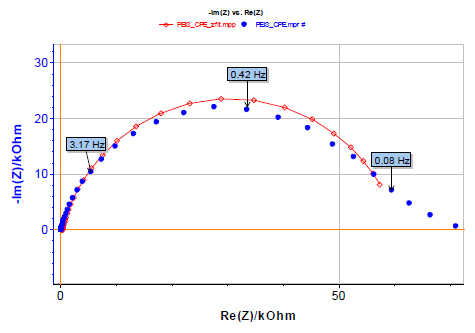
図5: 実験結果〔青色のマーカ〕とインピーダンスのフィッティング結果(赤色の曲線)
前述のように、フィッティングはR1+R2/Qの等価回路に従って実行されます(図6)。
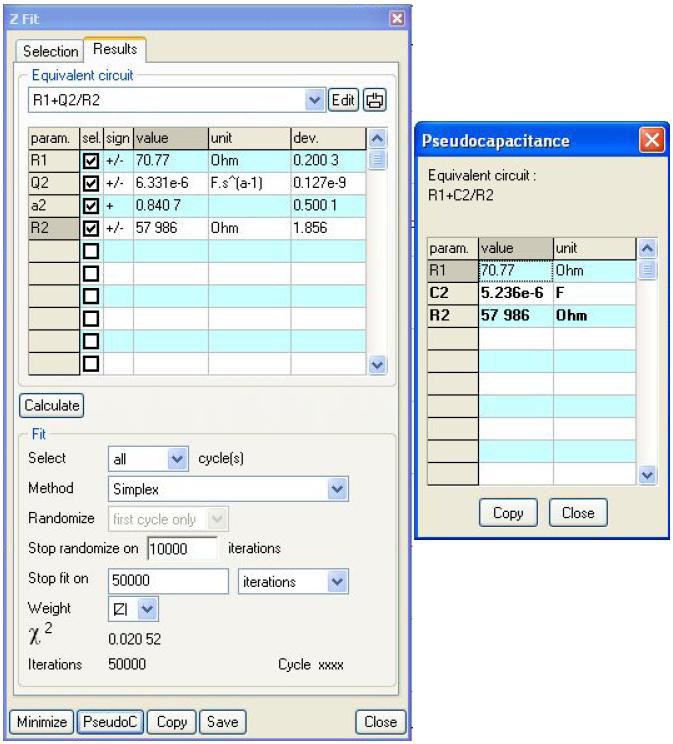
図6: 「Z fit」と「Pseudocapacitance」の結果
インピーダンスのフィッティング結果(赤色の曲線)
実験結果を見ると、溶液抵抗(R1 = RΩ = 71Ω)は、電荷移動抵抗(R2 = Rt = 58kΩ)と比較すると十分に小さいことがわかります。また、Qの値は6.3μF.sα-1、αは0.84です。
このとき、この実験系での静電容量は「Pseudocapacitance」というツールで計算され、Cdlは5.2μFと求められます(図6) [4]。
設定値と測定データは、EC-Lab®ソフトウェアのSamplesフォルダ内にあるPEIS_CPE.mprからロードすることができます。
Ⅴ- サイクリック・ボルタンメトリの結果と解析
Eocは、CVの実験を開始する前に測定され、その値はSCEに対して-0.235Vです。CV法のパラメータ(図7)は、掃引範囲はEocを中心とする±15mVで、掃印速度は40mV.s-1です。
1Rドロップは無視できる(前の章を参照)ので、Rpの値は曲線の傾きを計算することで求めることができます。

図7:サイクリック・ボルタンメトリのパラメータ設定
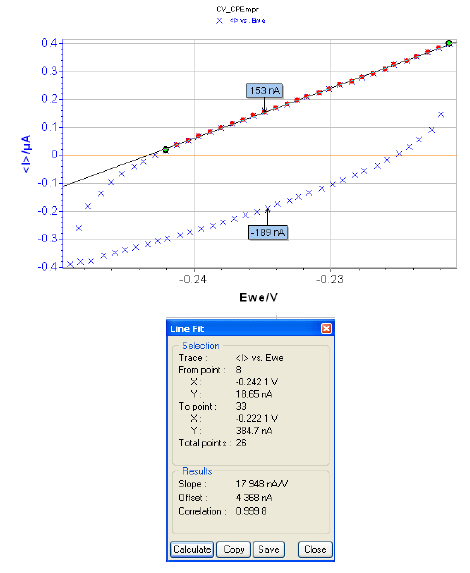
図8: 電位の増加方向への掃引および折り返し方向への掃引における定常状態曲線Ivs.EWE(上)とRpを特定するための「Line Fit」ツール(下)
電位の増加方向への掃印(図8)および折り返し方向への掃引から得られるRpの値は、それぞれ57kΩ(= 1/17.673 x 10-6)および61kΩで、PEISとCVによって求められたRpの値が一致していることがわかります。物質の拡散によって酸化還元過程の反応速度が制限されないため、次の式(2)が成立します([2])。

並列に接続された実際のキャパシタと抵抗によって、今回の実験系を模擬できると仮定すると、曲線のアノード部、カソード部それぞれの腐食電位に対応する2つの電流値IaおよびIcを求めることができます。これらの値を用いて、次の式により、二重層の静電容量を求めることができます。
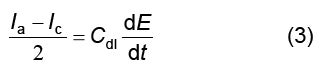
最後に、図8および式(3)から計算して、静電容量Cdlは4.3μFと求めることができます。
設定値と測定データは、EC-Lab®ソフトウェアのSamplesフォルダ内にあるCV_CPE.mprからロードすることができます。
ところで、回路R/Q(図3)のCV応答をシミュレーションにより求めることもできます。そのためには、CPEの電流応答が電位の線形変化に対応する関係式(4)を使用します。
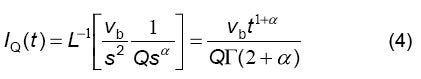
ここで、vbは電位の掃印速度、Γはオイラーのガンマ関数、Sはラプラス変数です。
EISデータを使用して測定したパラメータを使用したシミュレーション結果を図9に示します。
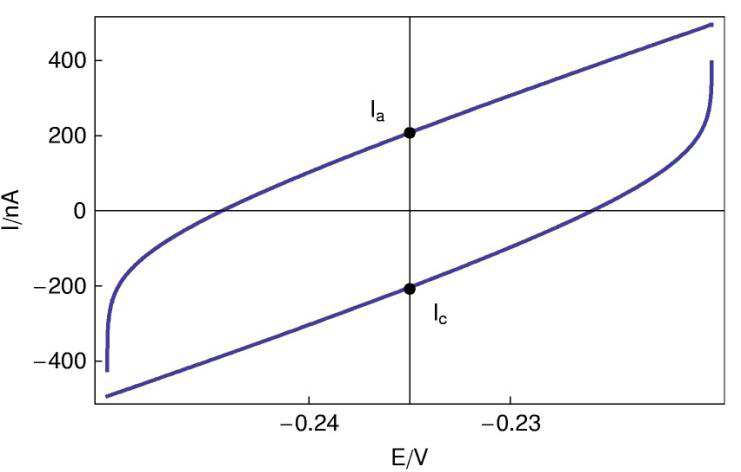
図9:Mathematicaソフトウェアによってプロットした回路R+R/Q(図3)のCVシミュレーション
Ia、Icを求め、式(3)を使用すると、Cdl = 5.2 x 10-6Fが得られ、これはEIS測定の結果から求めた値に対応しています。
Ⅵ- 結論
両方の手法(インピーダンス測定およびCV)によって求められた静電容量の値を、表1にまとめてあります。
静電容量の大きさは、どの手法により求めてもほぼ同じ(~ 5μF)となります。
ただし、CV測定から得られたデータの解析では、実際のキャパシタを用いた場合を前提としています。しかし、インピーダンス測定の結果を考えると、実際のキャパシタではなく、CPEを用いた等価回路により模擬されたため、この前提は検証されておらず、このことが2つの手法により求めた静電容量の値の差異の原因となっていると考えられます。
| 表1:要約 | ||||
|---|---|---|---|---|
| インピーダンス測定 | CV | |||
| (CPEの仮説) | 測定値 | シミュレート値 | ||
| Cdl/μF | 5.2 | 4.3 | 5.2 | |
参考文献
[1] Electrochemical methods.Fundamentals and applications, A. J. Bard, L. R. Faulkner, ed. Wiley (Hoboken), 2001.
[2] Cinétique électrochimique, J.-P. Diard, B. Le Gorrec, C. Montella, ed., Hermann (Paris) 1996.
[3] Impedance Spectroscopy.Theory, experiment and applications.E. Barsoukov, J.R.Macdonald, ed. Wiley (Hoboken), 1987.
[4] アプリケーション・ノート#20, https://www.biologic.net/document_type/application-notes/
- Bio-Logic社電気化学測定システム
- ・ハードウェア
- ・EC-Lab
- ・トラブルシューティング
- ソフトウェア
- ・Zviewおよび東陽テクニカ製ソフトウェア
- 電気化学測定
- ・基礎電気化学
- ・インピーダンス
- ・バッテリー
- ・腐食
- ・その他
- 燃料電池
- ・燃料電池評価







