FAMOS
レインフロー法に関するFAQ
Qレインフロー法概要
レインフロー法は、振幅の大きさを基準にクラスをカウントしていく手法です。
この振幅の大きさを考える手法は、屋根を流れる雨水の経路をイメージするとわかりやすいです。例として、下図のようなデータがあるものとします。
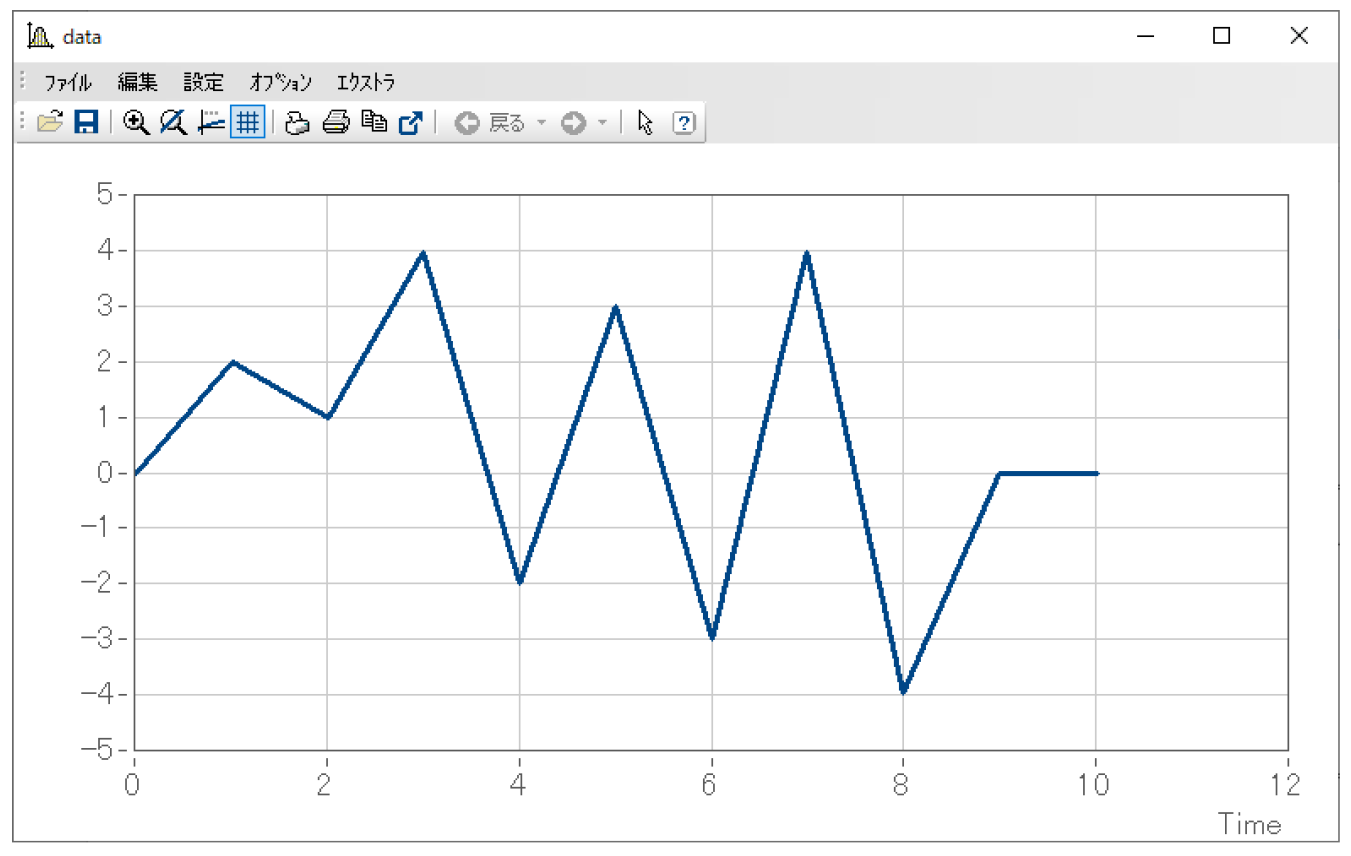
そして、時間軸を下方向にとった下図のような形で考えます。
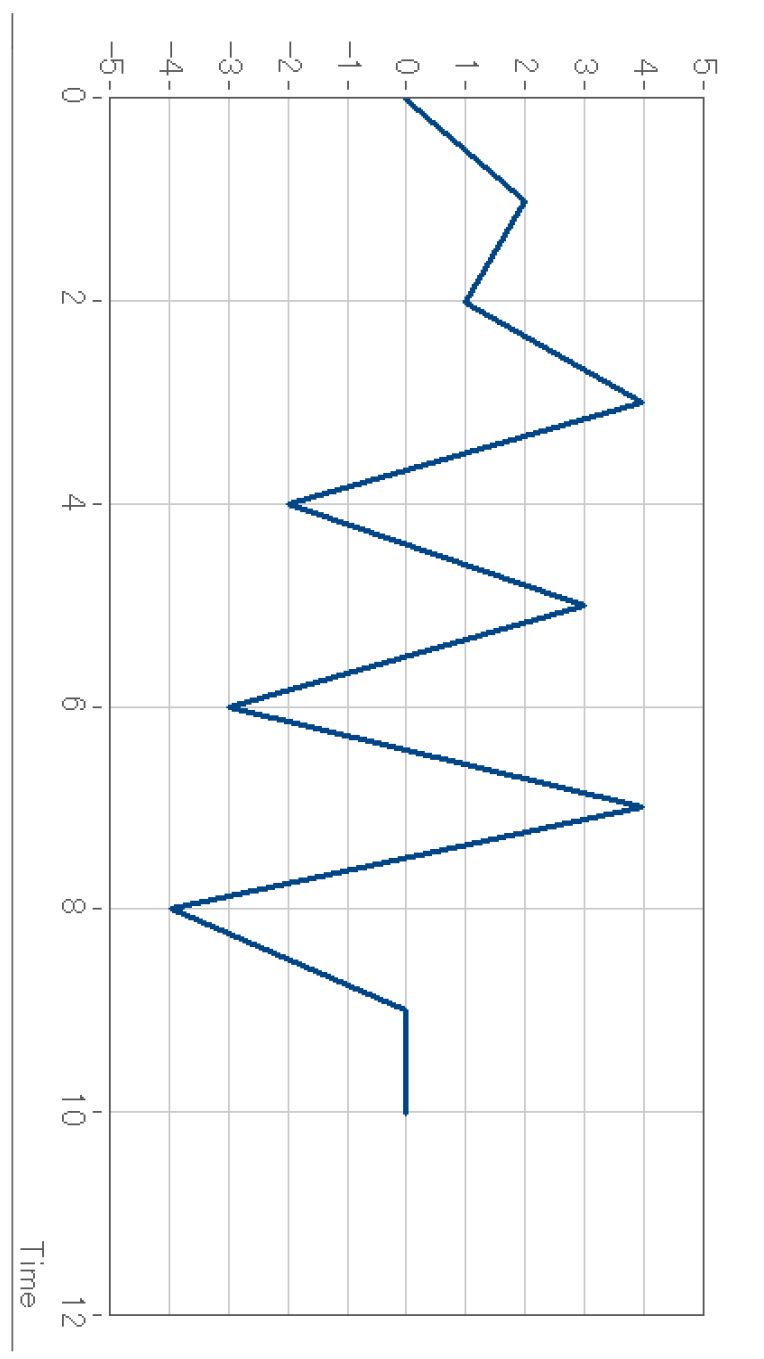
例えば、下図の赤〇、緑〇からのポイントから雨水が流れるとすると、図のような経路を取ることがイメージできます。雨水は、その他すべての極値(尖った点)からも同様に流れていきます。
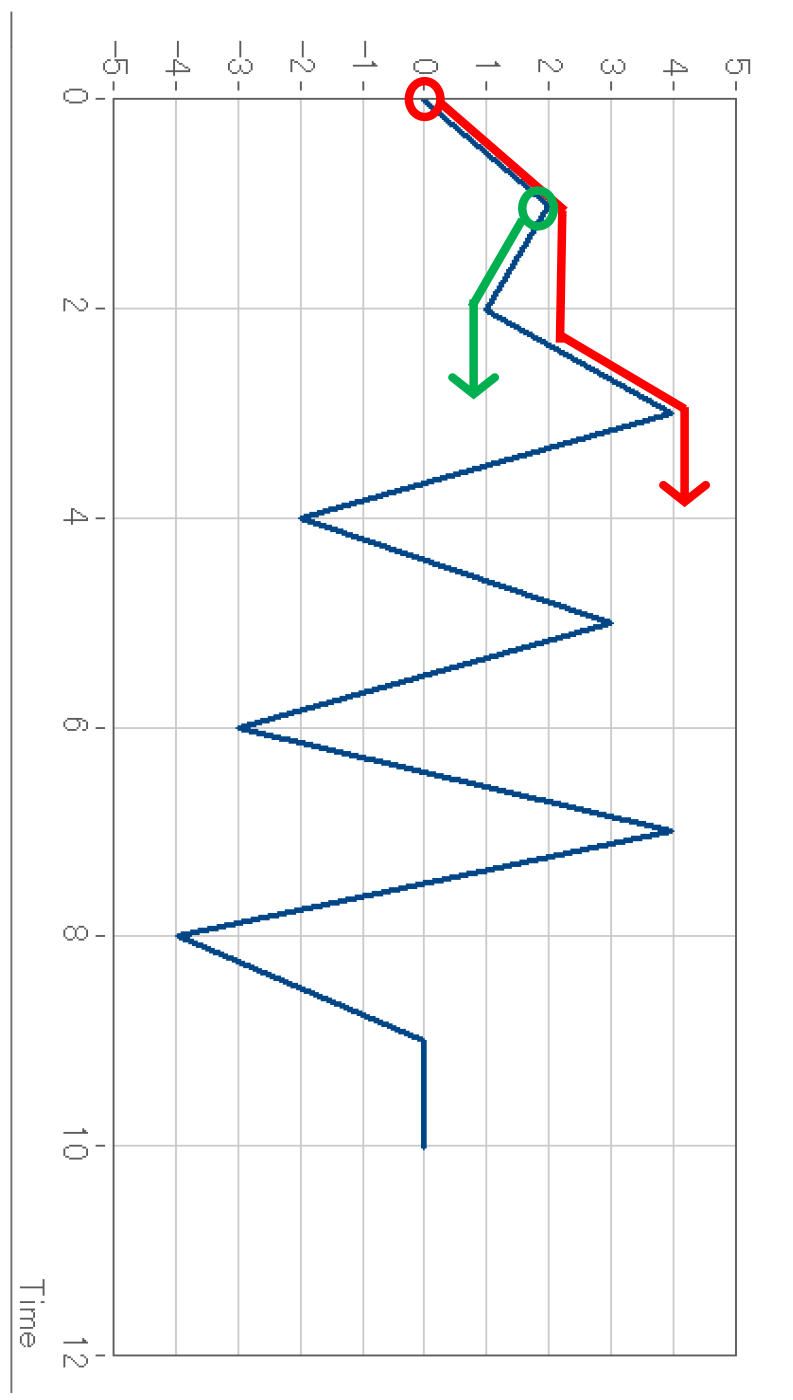
レインフロー法で重要となるのは、一度極値から流れ始めた雨水が、どの点で停止するかです。流れが始まった点、停止した点を使うことで、その経路での振幅を考えることができます。
雨水は、以下の2条件で停止します。
1)流れが右向きである場合、その出発点よりも、もっと左側に次の右向きの出発点がある場合。 (左向きの場合も同様、左右を読み替えて考える)
2)屋根に既に雨水が流れていた場合。
1)流れが右向きである場合、その出発点よりも、もっと左側に次の右向きの出発点がある場合。 の具体例を考えてみましょう。
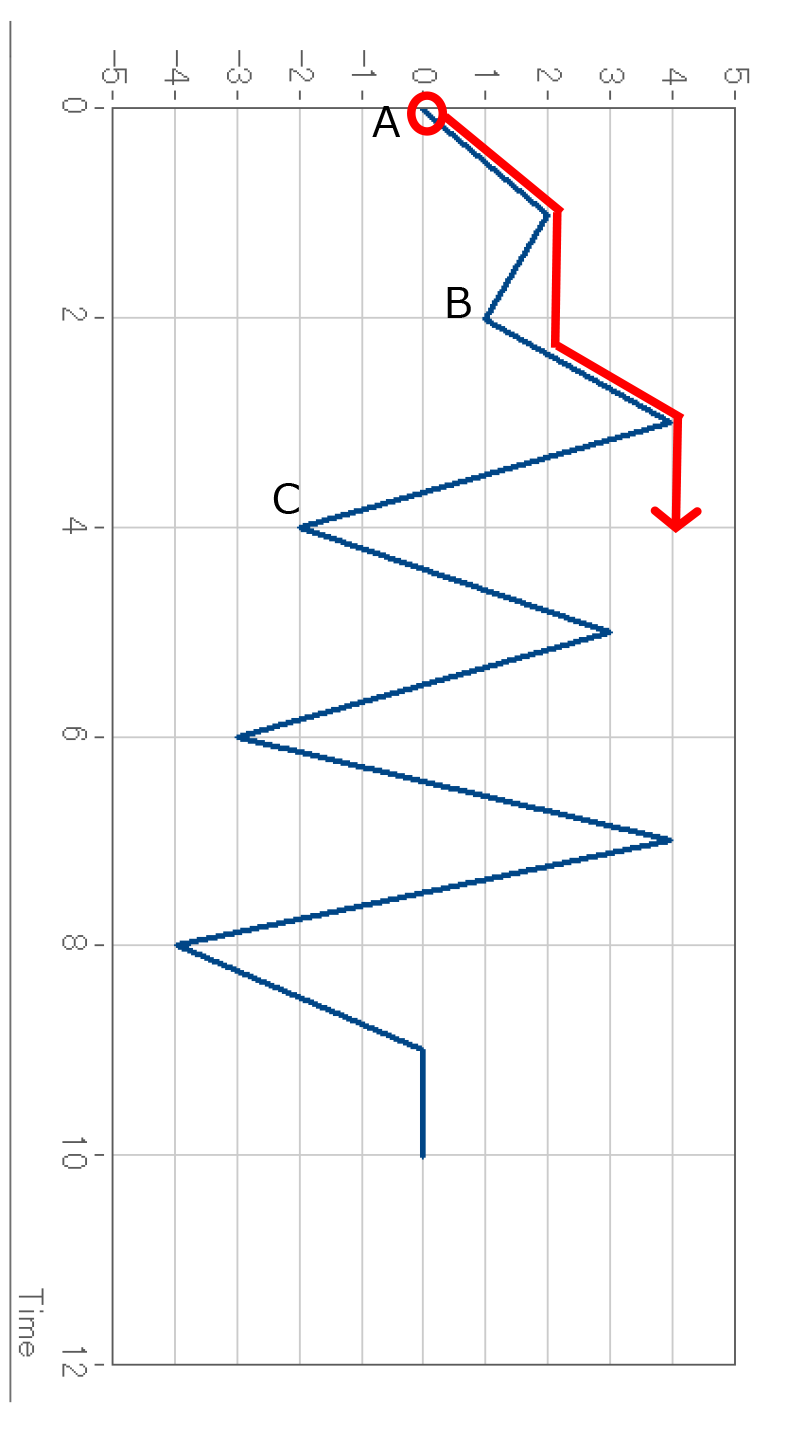
下図の点Aから流れた雨水は、このような経路を通ったうえでt=4である点で停止します。
これは、点Cが、点Aよりも左側にある、同じく右向きの出発点であるためです。
点Bも右向きの出発点ではありますが、「出発点よりも左側にある」という条件を満たさないため、ここでは停止しません。
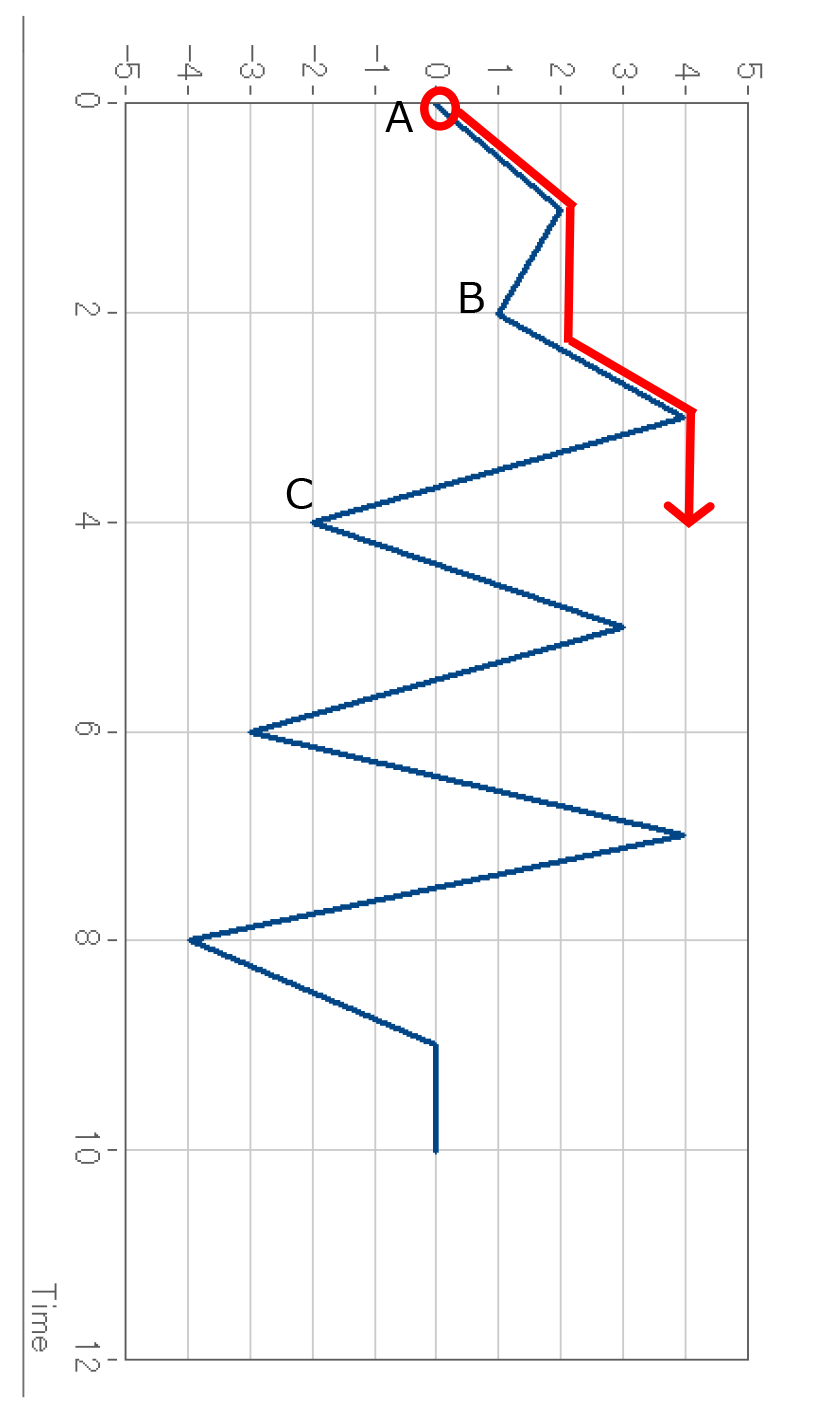
この流れの振幅は、出発点がy=0、停止点がy=4、という情報が使われます。
(実際の解析においてはこれらの値から振幅や平均値を求めます)
2)屋根に既に雨水が流れていた場合。
の具体例を考えてみましょう。
先ほどと同じく、下図の点Aから流れた雨水は、このような経路を通ったうえでt=4である点で停止します。
次に点Bから右向きに流れる雨水を考えると、これはすぐに点Aから流れた雨水とぶつかることになり、「屋根に既に雨水が流れていた場合」の条件を満たして停止します。
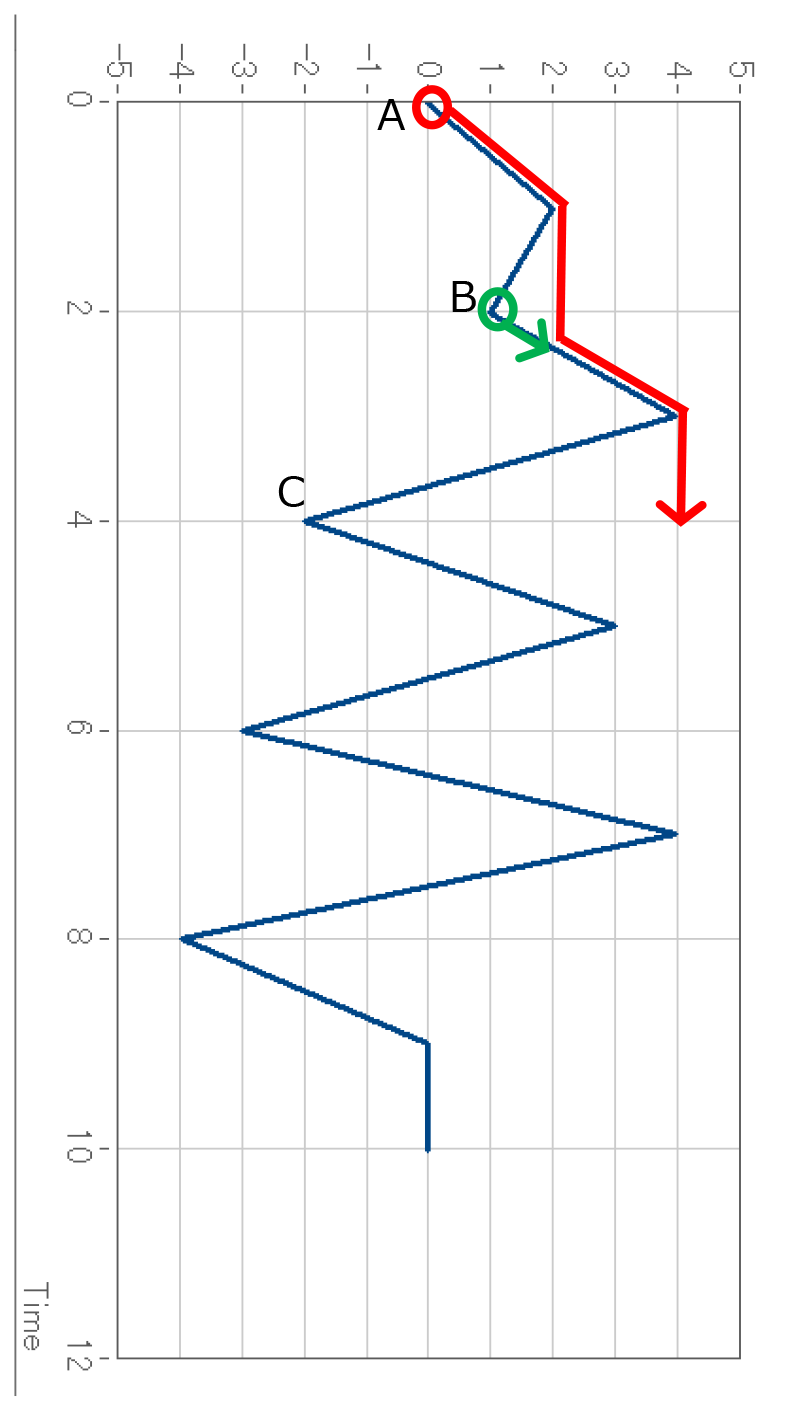
この流れの振幅は、出発点がy=1、停止点がy=2、という情報が使われます。
レインフロー法では、これらの出発点、停止点から「サイクル」という考え方を使います。ある振動が例えばy=0からy=4まで変化したとして、逆向きのy=4からy=0の変化があればそのセットが「1サイクル」です。片方のみの変化があればそれは「ハーフ(1/2)サイクル」として考えられます。
そのため、最終的な結果ではカウントとして0.5という数値が現れることがあります。これは、該当するクラスにおいてハーフサイクルがカウントされたことを意味します。
Q関数の記述例
レインフロー法は関係する関数が多く、結果の出力方法も何通りか存在します。
まずは基本的な関数の記述例全体をここで述べます。パラメータについては実際の値ではなく_(アンダーバー)付きの名前としています。
; レインフロー法の解析用パラメータの設定
ClsHandle = ClsOffRainflowInit1(_Classes, _UnitUse, _UnitColumn, _UnitRow, _UnitCounter,_Unit_Y_Residue, _SV_0)
ClsOffRainflowInit2(ClsHandle, _Min, _Max, _Hysteresis, _Axes, _Type, _OuterBins, _Calculation)
ClsOffRainflowInit3(ClsHandle, _IgnoreSmallSpans, _Precise, _CountStartEnd, _SV_Null1, _SV_Null2, _SV_Null3)
; 実際にカウント対象となるデータを与える
ClsOffRainflowFeedSamples(ClsHandle, Samples)
; レジデューを結果に加える
ClsOffRainflowAddResidue(ClsHandle, _Weight)
; 結果を返す
RainflowMatrix = ClsOffRainflowGetMatrix(ClsHandle)
; 結果を見やすい形に変換する
ResultRainflow = MatrixSumLines(RainflowMatrix, 0)
関数やパラメータ、変数が多いですが、要点である入力データと解析結果の変数はそれぞれ以下の通りです。
| Samples | カウント対象となる入力データ |
|---|---|
| RainflowMatrix | カウント結果、3次元の配列 |
| ResultRainflow | カウント結果を2次元配列に変換したもの |
クラスカウント法と大きく異なるのは関数の結果の形です。
関数記述例で「結果を返す」「結果を見やすい形に変換する」という箇所が存在する理由を説明します。
例として下図のようなデータを、レインフロー法と、クラスカウント法(ClsPeak2関数)で解析した結果を並べてみます。クラスの分類等、パラメータはなるべく同じように設定しています。
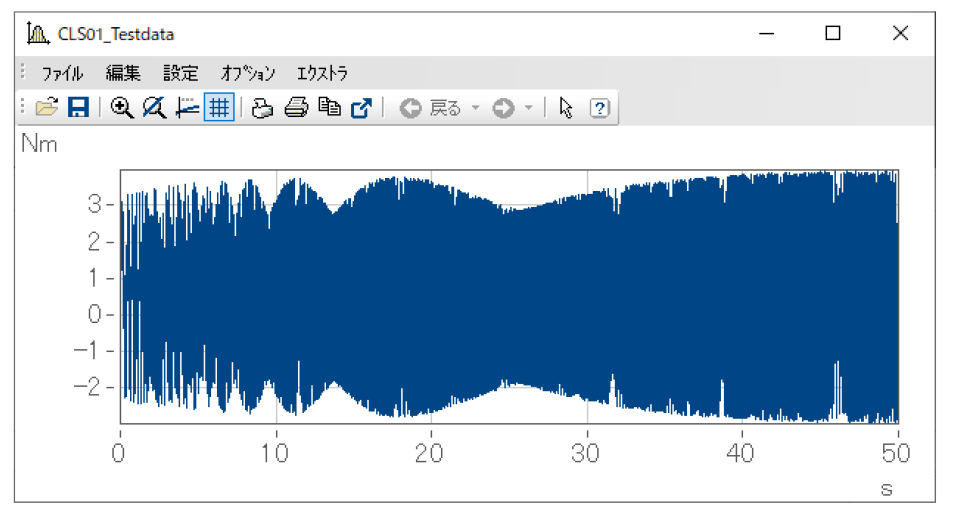
上がレインフロー法の結果(上記の関数記述例ではRainflowMatrixに当たるもの)、下がクラスカウント法の結果です。
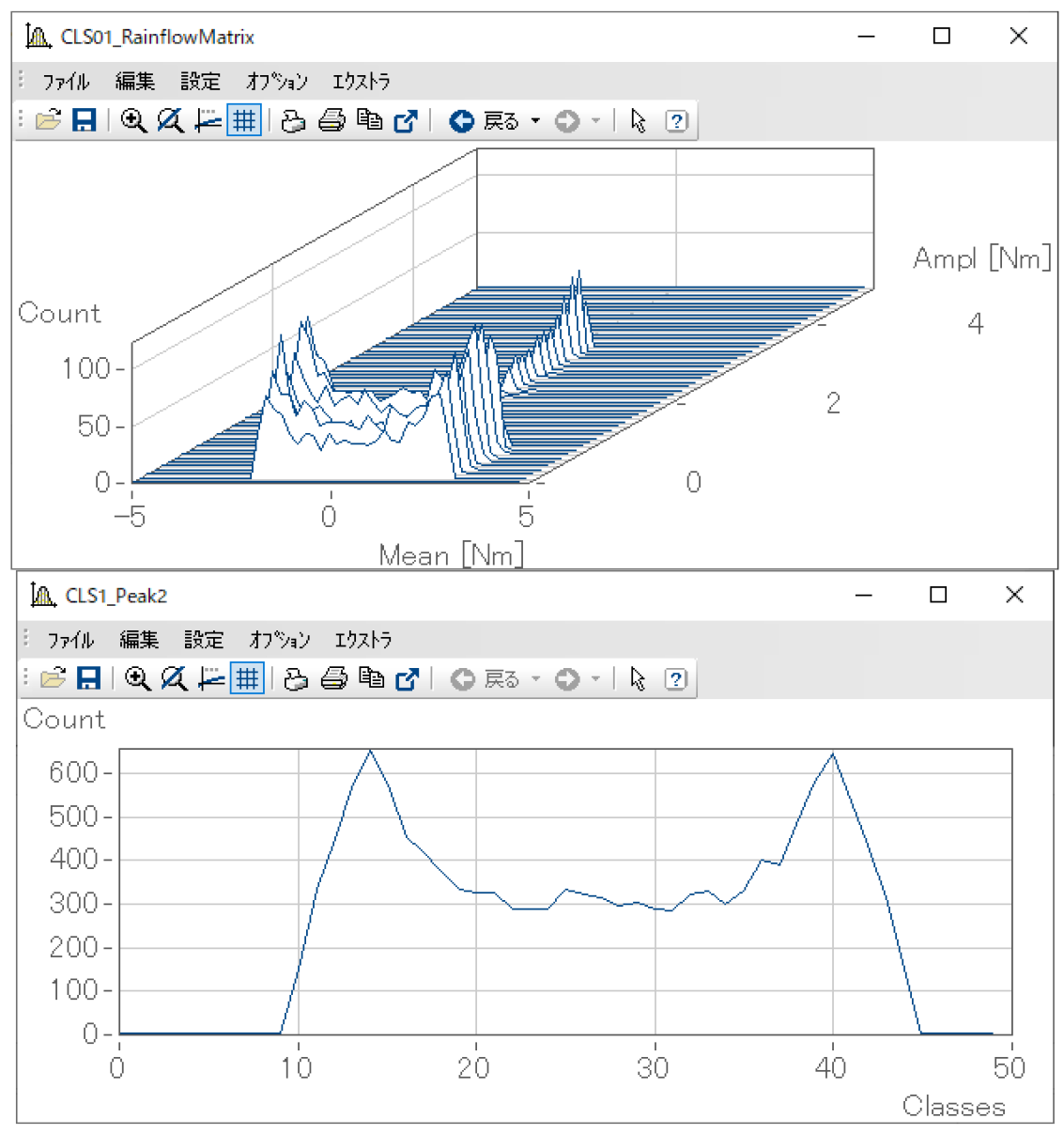
このように、クラスカウント法ではクラスとカウント結果の関係が2次元になるのに対して、レインフロー法では奥行き方向のZ軸も増えて3次元となります。通常、カウントされた後の結果としては2次元である方が後の処理(疲労寿命推定など)で扱いやすいため、関数記述例ではこの3次元から2次元への変換を「結果を見やすい形に変換する」としています。
なお、この図ではX軸はMean(平均)、Z軸はAmpl(振幅)としていますが、これらは関数のパラメータで設定されます。
QClsOffRainflowInit1 関数
ClsOffRainflowInit1関数は、レインフロー法の解析用パラメータを設定するための関数の1つです。パラメータは以下のようになります。
ClsHandle =ClsOffRainflowInit1(_Classes, _UnitUse, _UnitColumn, _UnitRow, _UnitCounter, _Unit_Y_Residue, _SV_0)
| ClsHandle | 以後の関数群が参照するための変数 (名称は任意) |
|---|---|
| _Classes | クラス数をいくつにするかの設定、4以上1000以下 |
| _UnitUse | クラス幅をどのようにスケーリングするかの設定 0:クラス番号でスケーリング(0, 1, 2...) 1:入力データ自体の物理単位でスケーリング |
| _UnitColmn | 結果のX軸の単位 (X軸の意味は後述) |
| _UnitRow | 結果のZ軸の単位 (Z軸の意味は後述) |
| _UnitCounter | 結果のY軸の単位 (Y軸はカウント回数) |
| _Unit_Y_Residue | レジデューのY軸の単位 (基本的にカウント回数) |
| _SV_0 | 常に0に設定しておく現在は使われていないパラメータ |
〇軸の単位、というパラメータは表記上の文字列の設定です。
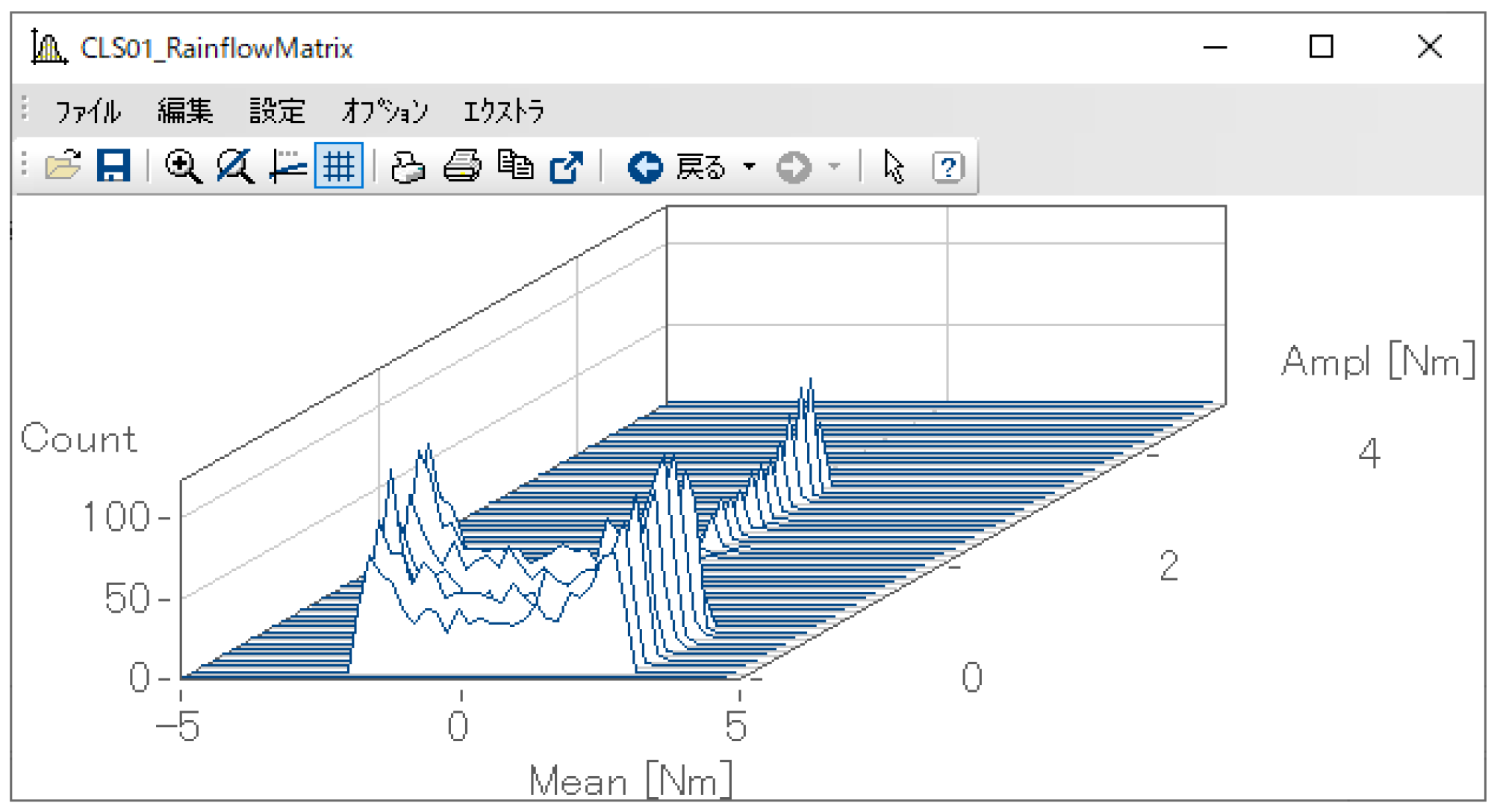
例えば下図の結果の場合、X軸の単位はMean [Nm]、Z軸の単位はAmpl [Nm]、Y軸の単位はCountという文字列がそれぞれ設定されています。ここでのX軸、Z軸の設定はあくまで表記上の文字列のみであり、実際の軸の意味自体はClsOffRainflowInit2関数で設定します。
クラス幅のスケーリング、_UnitUseは1、つまり入力データ自体の物理単位によるスケーリングが使用されています。
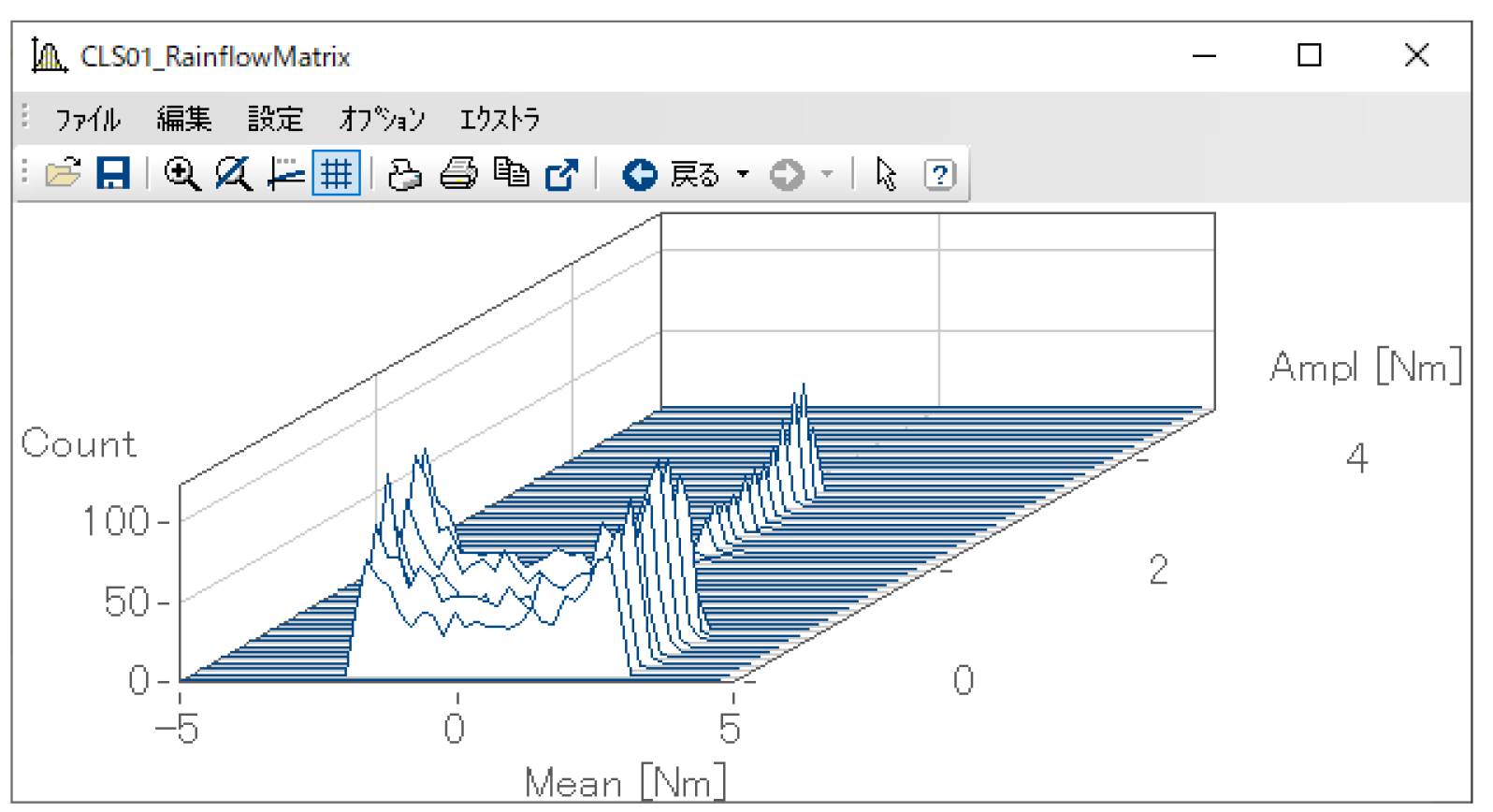
これ単体では解析用パラメータの設定は完結せず、ClsOffRainflowInit2、ClsOffRainflowInit3関数へ続きます。続く関数では、この関数で作成される変数であるClsHandleを参照します。
QClsOffRainflowInit2 関数
ClsOffRainflowInit2関数もClsOffRainflowInit1関数と同様、レインフロー法の解析用パラメータを設定します。パラメータは以下のようになります。
ClsOffRainflowInit2(ClsHandle, _Min, _Max, _Hysteresis, _Axes, _Type, _OuterBins, _Calculation)
| ClsHandle | ClsOffRainflowInit1関数で作成された変数 |
|---|---|
| _Min | クラスの下限 |
| _Max | クラスの上限 |
| _Hysteresis | 小さな振動を無視するためのヒステリシスの大きさ、1つのクラス幅が推奨値 ヒステリシスの考え方については「ClsPeak1関数 関数のパラメータ」参照 |
| _Axes | X軸にどのような意味を割り当てるかの設定、詳細後述 |
| _Type | X軸、Z軸にどのような意味を割り当てるかの設定、詳細後述 |
| _OuterBins | クラスの上限/下限の外にある値をどのように扱うかの設定、詳細後述 |
| _Calculation | 解析用のアルゴリズムの設定、詳細後述 |
軸の意味を設定するパラメータ、_Axes、_Typeを説明します。まずはパラメータの設定可能な値と内容だけ並べてみます。
[_Axesの設定値] X軸の意味
0:ターゲットクラスまたは振幅
1:平均またはスタートクラス
[_Typeの設定値] X軸とZ軸の意味
0:スタートクラスとターゲットクラス
1:振幅と平均
2:平均とスパン
これらのパラメータは組み合わせで内容が決定されます。
例えば_Typeの値を1とした場合、これは「X軸とZ軸はどちらかが振幅、どちらかが平均を意味する値となる」という設定です。
次に_Axesを考えましょう。ここで_Axesを1とすると、「X軸の意味は振幅/平均のうちの平均である」と決まります。自動的にZ軸が振幅となります。
このように_Axes、_Typeは組み合わせることでX軸は何を意味する軸か、Z軸は何を意味する軸か、がそれぞれ決定されます。
次はここで出てくる単語、スタートクラス、ターゲットクラス、振幅、平均、スパン、の意味をそれぞれ見ていきましょう。
「レインフロー法概要」でも触れましたが、レインフロー法には「流れの始点」「流れの終点」の概念が存在します。
下図の例では点Aから始まる流れはy=0が始点、y=4が終点です。これらのy=〇ポイントは、それぞれいずれかのクラスに分類されているはずです。
軸の意味で出てくる単語は、それぞれ下記を意味します。
| スタートクラス | 流れの始点が分類されるクラス |
|---|---|
| ターゲットクラス | 流れの終点が分類されるクラス |
| 振幅 | (スタートクラス – ターゲットクラス)/2 の絶対値 |
| 平均 | (スタートクラス – ターゲットクラス)/2 |
| スパン | (スタートクラス – ターゲットクラス) |
残る_OuterBinsと_Calculationの設定値を見ていきましょう。
_OuterBinsはクラスの上限/下限の外にある値の扱いに関する設定です。
0:クラスの上限/下限の外にある極値は無視されます。
1:クラスの上限/下限の外にある極値は、クラス内に割り当てられます。(こちらが推奨設定)
_Calculationは解析用のアルゴリズムの設定です。これらは規定のアルゴリズムであるためその中身は詳しく説明せず、アルゴリズムの名称等のみ述べます。
0:標準的な4点アルゴリズム (standard-algorithm 4 points)
1:コールマンシーガ補正 (Chlormann Seeger correction)
2:1990年に再承認されたASTM E1049に基づいた計算
3:RAINFLOW-HCMメソッド (U.H. Clormann, T. Seeger; Stahlbau 3/1986)
_Calculationとして2を選択した場合、後述するClsOffRainflowAddResidue関数を呼び出す必要があります。また、ClsOffRainflowInit3関数における_Preciseのパラメータは無視されます。
_Calculationとして3を選択した場合、ClsOffRainflowInit3関数における_Preciseのパラメータは無視されます。
QClsOffRainflowInit3 関数
ClsOffRainflowInit3関数もClsOffRainflowInit1関数と同様、レインフロー法の解析用パラメータを設定します。パラメータは以下のようになります。
ClsOffRainflowInit3(ClsHandle, _IgnoreSmallspans, _Precise, _CountStartEnd, _SV_Null1, _SV_Null2, _SV_Null3)
| ClsHandle | ClsOffRainflowInit1関数で作成された変数 |
|---|---|
| _IgnoreSmallSpans | 1つのスパンに収まる小さなスパンを無視するかどうか |
| _Precise | クラスの上限 |
| _CountStartEnd | 小さな振動を無視するためのヒステリシスの大きさ、1つのクラス幅が推奨値 |
| _SV_Null1 | 常に0に設定しておく現在は使われていないパラメータ |
| _SV_Null2 | 常に0に設定しておく現在は使われていないパラメータ |
| _SV_Null3 | 常に0に設定しておく現在は使われていないパラメータ |
_IgnoreSmallSpans、_Precise、_CountStartEndは特定の値を選択するパラメータです。
_IgnoreSmallSpansは、1つのクラス内に収まってしまう小さなスパンをどのように扱うかの設定です。
0:小さなスパンもカウントします。
1:小さなスパンを無視します。
_Preciseは、スパンをどれほど精度良く計算するかの手法の設定です。
0:極値は最初にクラスに割り当てられ、次に振幅/平均の計算において振幅/スパンは引き算により求められますが、これはあまり正確ではありません。
1:スパンと平均値を正確に計算し、それに基づいてクラスに関連させます。
2:1と同様の処理に加えて、より正確にレジデューから削除を行います。
3:2と同様の処理に加えて、レジデューが消える場合にも正確に削除を行います。
4:3の処理に近いですが、ClsOffRainflowFeedSamples関数が複数回呼ばれた場合であっても、丸めずに正確なレジデューを追加します。
5:4の処理に近いですがより正確です。
特別な理由が無い限りは_Preciseの設定は5を推奨します。 ClsOffRainflowInit3関数の_Calculationにおいて2または3(ASTM E1049、HCM)を選択している場合はこの_Preciseのパラメータ設定は無視され、5と同じ動きとなります。
QClsOffRainflowFeedSamples関数
ClsOffRainflowFeedSamples関数は、実際にレインフロー法でカウントを行う対象データを与えるための関数です。パラメータは以下のようになります。
ClsOffRainflowFeedSamples(ClsHandle, Samples)
| ClsHandle | ClsOffRainflowInit1関数で作成された変数 |
|---|---|
| Samples | 解析対象とするデータの変数 |
この関数は複数回実行することができます。例えば試験をN回行っていてそのN回分のデータをまとめて1つのカウント結果としたい場合、この関数をN回繰り返すことで実行できます。
QClsOffRainflowAddResidue関数
レインフロー法におけるカウントでは、1回分のカウントに満たない成分がレジデュー(Residue)として扱われます。この関数ではこのレジデューを最終的なカウント結果にどのように反映させるかの設定を行います。パラメータは以下のようになります。
ClsOffRainflowAddResidue (ClsHandle, _Weight)| ClsHandle | ClsOffRainflowInit1関数で作成された変数 |
|---|---|
| _Weight | カウント結果に反映させるための重み |
_Weightとしては0~1の範囲の値が設定可能ですが、実際に入力するべき値としては3通りです。
0:レジデューの値はカウント結果には反映されません。
0.5:レジデューの値はハーフサイクルと同じものとしてカウント結果に反映されます。
1:レジデューの値は1サイクルと同じものとしてカウント結果に反映されます。
つまり、_Weightが1に近いほどカウントの結果が大きくなります。
なお、ClsOffRainflowInit3関数の_Calculationにおいて2 (ASTM E1049)を選択している場合は、このアルゴリズム自体でレジデューの扱いが定義されているため、この_Weightのパラメータ設定は無視されます。
QClsOffRainflowGetMatrix関数
ClsOffRainflowGetMatrix関数は、ここまでの関数により設定された解析方法、与えられたデータによるカウント結果を返すための関数です。記述は下記のようになります。
RainflowMatrix = ClsOffRainflowGetMatrix(ClsHandle)
ここで、式の左辺は結果の変数の名前、ClsHandleはClsOffRainflowInit1関数で作成された変数です。
この関数で得られる結果は、下図のような奥行き方向の存在する3次元データです。
X軸、Z軸にどのような意味が割り振られるかは、ここまでに説明した関数で決定されます。
QMatrixSumLines関数
MatrixSumLines関数はレインフロー法とは直接関係の無いもので、3次元データの編集を行うための関数です。この関数を利用することで、本来3次元であるレインフロー法の解析結果を、クラスカウント法のような2次元の結果に変換することができます。なお、疲労寿命推定は3次元データのままで計算可能です。
結果の表示や出力の際に見やすい形とするために利用できます。
記述は下記のようになります。
ResultRainflow = MatrixSumLines(RainflowMatrix, 0)
ここで、式の左辺は結果の変数の名前、RainflowMatrixはClsOffRainflowGetMatrix関数で作成された3次元のカウント結果の変数です。末尾の数値は0または1が設定できます。
末尾の0または1に応じて、3次元の結果をX軸、またはZ軸方向にまとめて2次元の結果に変換します。
例として下図のようなMean, AmplをX軸、Z軸として持つ3次元データにこの関数を適用してみます。
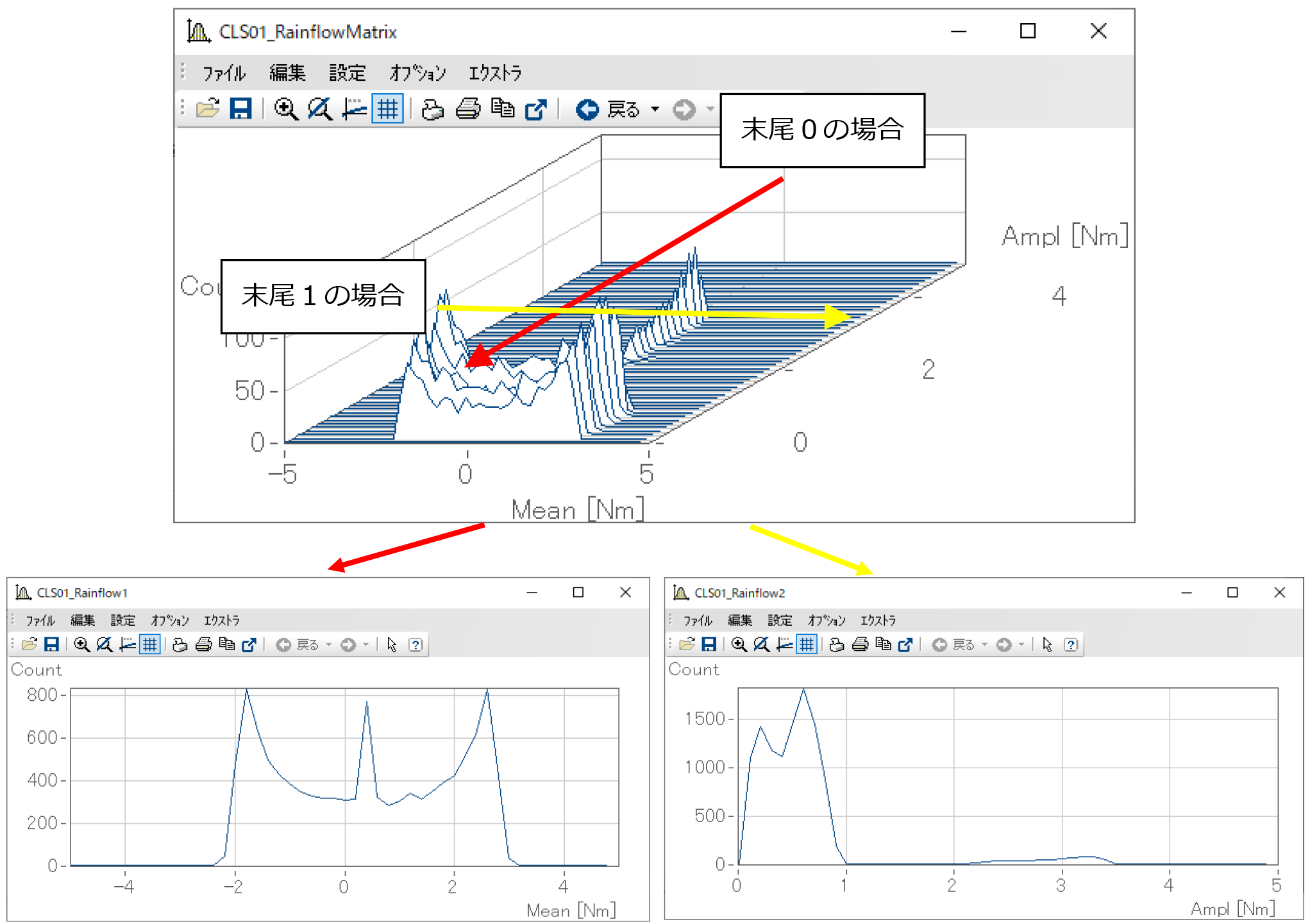
末尾が0の場合、X軸方向にすべての結果が合算され、左側のようにMean-Countの2次元のカウント結果となります。同様に末尾が1の場合、Z軸方向にすべての結果が合算され、右側のようにAmpl-Countの2次元のカウント結果となります。ここまでの関数を利用することで、X軸、Z軸をどのように設定するか、最終的な結果をどちらにまとめるか、を任意に設定可能です。