FAQ
OROS社 OR3x
プラグイン
└FFT
ID.x118
Q. FFTアナライザの平均方法であるエクスポネンシャル平均とは?
FFTアナライザの平均方法として”エクスポネンシャル平均”という項目がありますが、これに設定すると指定回数を超えても停止しません。どのような方法なのか教えてください。
A.
【リニア平均】
指定回数を設定してFFT解析を開始すると、毎回の解析結果の平均を求めます。また、指定回数に達すると解析は終了します。
【エクスポネンシャル平均】
指定回数分の解析結果に対して指数重みを掛けて平均を求めます。指定回数に達しても解析を終了せずに終了が指示されるまで解析を繰り返します。
指定回数に達成してもFFT解析を終了しないので、ランニング平均と呼ばれることもあります。
各々の算出方法は以下の通りです。
【リニア平均】
リニア平均の場合、以下のように計算を行います。
Yn=( X1 + X2 + X3 + ...... Xn)/N
ただし、
N : 平均回数
Yn : N回の平均結果
Xn : 毎回の解析結果
上式からも明らかなように各解析結果に対して等しい重みで平均を求めます。また、指定回数に達した場合に解析を終了します。
ここで、計算式を以下のように変形します。
Yn =( X1 + X2 + X3 + ...... Xn-1 + Xn)/N ------(1)
Yn-1=(X1 + X2 + X3 + ...... Xn-1)/(N-1) -------(2)
式(1)から式(2)を引くと以下のように変形できます。
Yn =(1/N)Xn + (N-1)/N ・ Yn-1 ------(3)
【エクスポネンシャル平均】
式(3)に対して、ここでは式を簡単にするために1/N=Aとします。
Yn =A・Xn + (1-A) ・ Yn-1
指定回数で解析を終了させず、常に計測を続けると考え、指定回数分の平均を行った場合には、式を展開して以下のようになります。
Yn =A・Xn + (1-A)・Yn-1
=A・Xn + (1-A)・{A・Xn-1 + (1-A)・Yn-2}
=A・Xn + (1-A)・A・Xn-1 + (1-A)2・n-2
=A・Xn + (1-A)・A・Xn-1 + (1-A)2・{A・Xn-2 + (1-A)・Yn-3}
=A・Xn + (1-A)・A・Xn-1 + (1-A)2・A・Xn-2 + (1-A)3・Yn-3}
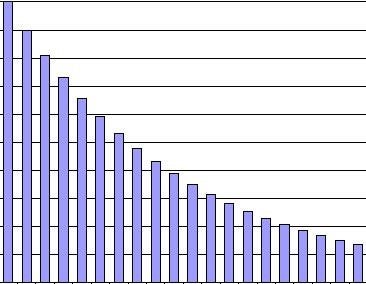
上式では3回分しか計算しませんでしたが、各解析結果に対する重みが指数で掛ります。
例えば、A=0.1とした場合には、以下のようになります。
Yn =0.1・Xn + 0.9・0.1・Xn-1 + 0.92・0.1・Xn-2 + ......
=0.1・Xn + 0.09・Xn-1 + 0.081・Xn-2 + ......
このときの重みをグラフで示します。このように重みが指数関数となります。