経時変化する系におけるインピーダンス解釈の問題点
I- はじめに
稼動中の電池や腐食反応のような電気化学系は、時間に対して不変であることはほとんどありません。経時変化する系で測定したインピーダンススペクトルに対して等価回路解析を行うと、誤った解釈が得られる恐れがあります。本章では、経時変化する可変抵抗を備えた等価回路を用いて、誤った解釈に至る例を2つ示します。
II 経時変系のインピーダンスプロット
II.1 R1+R2(t)/C2回路(R2が経時的に増加)
稼動中の電池や腐食反応のような経時変化を伴う測定系の変化の様子は、経験的にわかるものではなく予測することができません。 図1に示すR1+R2(t)/C2回路[2]を考え、次の関係(1)に従い時間と共に増加する抵抗R2を考えます。
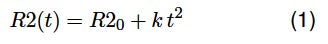
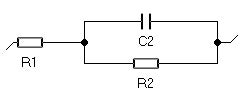
図1: R1+R2(t)/C2回路
インピーダンスは、1周期の正弦波信号を使って測定され、合わせて計算されます。インピーダンスは、1周期の正弦波信号を使って測定され、次の式によって与えられる時間tでの抵抗値R2を使用し、周波数fnで計算されます。
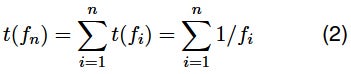
t(fi)は、ある周波数における1点の測定時間、すなわちその測定周波数の逆数です([3])。 周波数掃引は、fmax → fmin(fmax = 10Hz、fmin = 10−3Hzとする)の範囲で行い、測定周波数はログスケールで1桁あたり8点とします。また、R1、R2、およびC2に用いる値は図2のキャプションを参照してください。
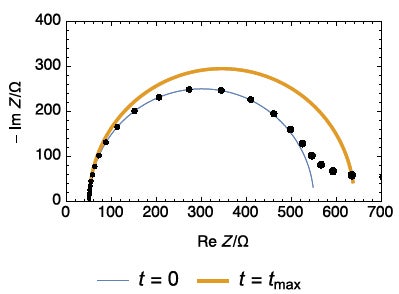
図2: 回路R1+R2(t)/C2 (R1 = 50Ω、R20 = 500Ω、k = 10-5Ω s-2、C2 = 2 × 10-2F)から得られる瞬間のナイキスト線図(t = 0、t = tmax)と経時変化をシミュレーションしたナイキストプロット(●)。なおドットのサイズは時間の経過に伴い大きく記載しています。
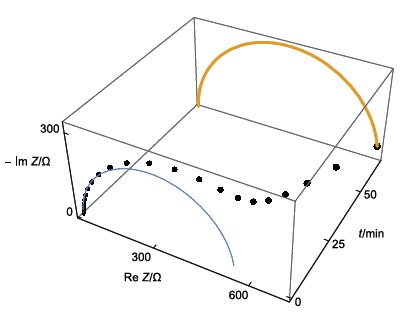
図3: 図2の3次元表示
この系に対してシミュレーションにより得られるナイキスト線図を図2および図3に示します。図2では低周波側に円弧の始まりのようなプロットが見られます。ここで、図4に示す等価回路を考えると、この経時変化しない回路のインピーダンスは、図1の経時変化する回路のインピーダンスに類似したグラフとなります。
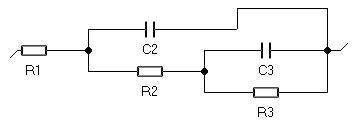
図4: R1+C2/(R2 +C3/R3)回路
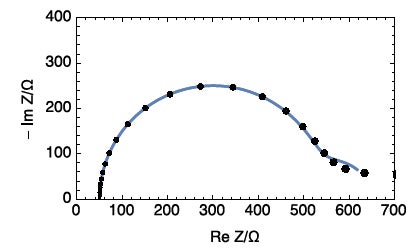
図5:経時変化する系R1+R2(t)/C2のナイキスト線図(●)と経時変化しない系R1+C2/(R2+C3/R3)のナイキスト線図。ただし、R1 = 50Ω、R2 = 500Ω、C2 = 10-2F、R3 = 100Ω、C3 = 1F
両方のグラフを比較した図5を見ると、これらが類似していることがわかります。これは、測定系が経時変化していることを知らない測定者が、必要以上に複雑な等価回路を用いて間違った解析をしてしまう恐れがあることを示しています。
II.2 R1+R2(t)/C2 (R2が経時的に減少)
抵抗R2の経時変化による次の2つ目の事例を図6に示します。抵抗R2の値はこれ以降、次の式(3)に従い時間の経過と共に減少するものとします。
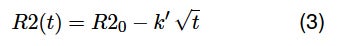
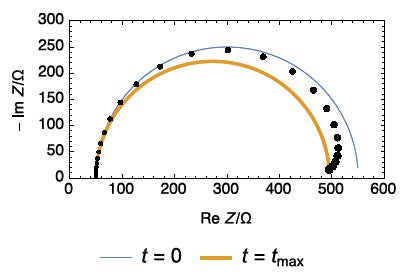
図6: 回路R1+R2(t)/C2 から得られる瞬間のナイキスト線図(t = 0、t = tmax)と経時変化をシミュレーションしたナイキストプロット(●)。
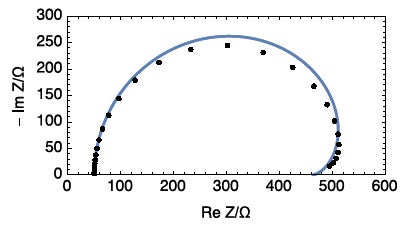
図7: 経時変化する系R1+R2(t)/C2のナイキスト線図(_)と経時変化しない系
R1+C2/(R2+C3/R3)のナイキスト線図。
ただし、R1 = 50Ω、R2 = 534:375Ω、C2 = 1.1 x 10-2F、R3 = -123.75Ω、C3 = -0.125F。
なお、図4の回路はR3 < 0かつC3 < 0のとき、図8の回路R1+C2/R2/(R3’+L3) (R3 > 0かつL3 > 0)に変換できます。ただし、R3’とL3は次の式(4)より得られます。
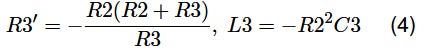
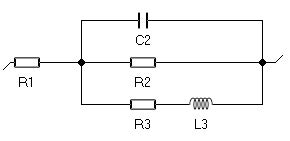
図8: R1+C2/R2/(R3’+L3)
III システムの定常性のチェック
III.1 Kramers-Kronig(KK)変換
KK変換を使用して求めたインピーダンスZKKを図9に示します。ZおよびZKKのナイキスト線図は、すべての周波数で類似しているわけではありません。このことから、インピーダンス測定が経時変化しない系で行われていないことがわかります。
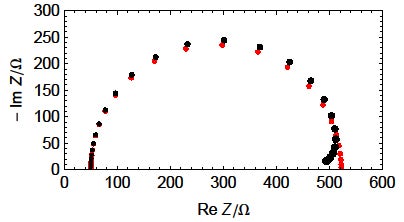
図9: R1+R2(t)/C2の測定で得られるナイキスト線図のシミュレーション(●)と、KK変換を使用して得られたナイキスト線図(●)
III.2 連続測定
より簡単に系の不変性を確認する方法として、同じ測定を2回連続的に実施する手法があります(図10)。さらにひと工夫として、周波数をfmax → fmin と減少する方向に掃引して測定した後、すぐにfmin → fmaxと周波数が増加する向きに掃引し、2つのインピーダンス測定を連続的に実施することも有効です。(図11)。
図10および11に示した2つのインピーダンス図は異なっており、これにより測定対象の系が時間的に変化していることがわかります。
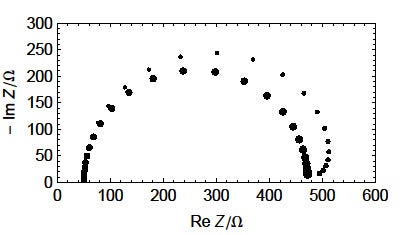
図10: R1+R2(t)/C2のナイキスト線図(fmax → fminに周波数を掃引し、2回連続的にインピーダンス測定を実施)
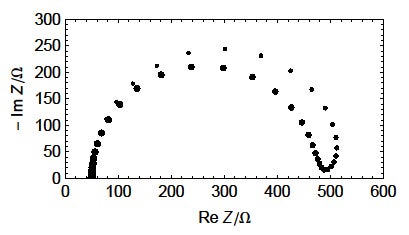
図11: R1+R2(t)/C2ナイキスト線図(fmax → fmin → fmaxと周波数を掃引し、2回の連続したインピーダンス測定を実施)
IV 結論
インピーダンス測定結果の解析を行う前に、系の不変性を確認することは非常に重要です。系が経時変化する場合インピーダンスの測定結果は複雑になり、解析に用いる等価回路も不必要に複雑になってしまう恐れがあります。
東陽テクニカでは、経時変化するサンプルのインピーダンスを3D(実数軸・虚数軸・時間軸)でプロットし、ある瞬間のインピーダンスデータを決定・解析するためのソフトウェアを開発しました。
詳細は、下記のリンクをご確認ください。
▶Z-3D 3Dインピーダンス解析ソフトウェア
参考文献:
[1] アプリケーション・ノート#9.Linear vs. non linear systems in impedance measurements.
www.bio-logic.info/potentiostat/notesan.html.
[2] Z. STOYNOV and B. SAVOVA-STOYNOV, J. Electroanal.Chem.183, 133 (1985).
[3] F. BERTHIER, J.-P. DIARD, A. JUSSIAUME, and J.-J. RAMEAU, Corrosion Science 30, 239 (1990).
[4] J.-P. DIARD, B. LE GORREC, and C. MONTELLA, Cin´etique´electrochimique, Hermann, Paris, 1996.
[5] アプリケーション・ノート#15.Two questions about Kramers-Kronig transformations.
www.bio-logic.info/potentiostat/notesan.html.
お問い合わせ
株式会社東陽テクニカ 理化学計測部