クーロン効率測定における精度と確度
クーロン効率測定における精度と確度
本書はBiologic社が発行するApplication note #53を2020年8月において翻訳したものです。
今後、原文が改訂され、内容が変更された場合には、改訂後の原文の内容を優先いたします。
1.はじめに
近年、電池寿命に関する研究でクーロン効率(CE)測定が注目を集めています[1-8]。 従来の単純な充放電サイクル試験下で、電極/電解液が変化することによる電池寿命への影響を定量化するためには非常に長い時間が必要です。従来の充放電サイクル試験に対し、CE測定を用いることで3-4週間と短い期間で電池寿命への影響を定量化できます。また、異なるセルの安定性を比較/評価することもできます。
CEの定義は(1)式のようにQdisとQchの比で表されます。Qdisは放電中の電気量、Qchは充電中の電気量です。
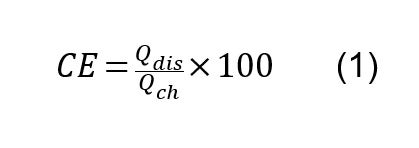
1-1.CE測定の精度と確度
数週間で電極材料や電解液の電池寿命への影響を評価するには、高精度2と高確度3で計測することが求められます。CE測定の精度は容量:Qの測定精度に影響されます。充放電中で放出/蓄積される電荷はQdis/ch=IxΔtで定義4されます。Iは充放電中の流れる電流で、Δtは充放電にかかる時間です。電圧変動は充放電の温度など様々な現象に影響されます。そのため容量:Qの測定は電流・電圧の測定精度、充放電時間の正確性、温度変化などの異なる要因に影響されます。
文献[2,4]ではCEデータ(vsサイクル数)を2次多項式関数(最小二乗回帰)でフィッティングすることによりCE測定の品質を定量化しました。フィッティング後、二乗平均平方根誤差(RMSE)は、次のように計算することができます。
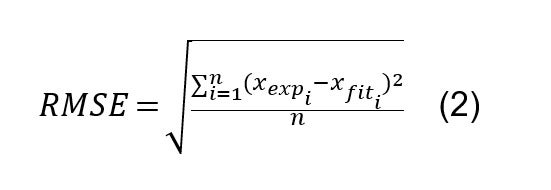
2.CE測定
2-1.実験条件
本アプリケーションノートの実験で使用された商用電池は下記の通りです
| LiNixMNyCozO2 (NMC) |
18650型 | 公称容量2.6 Ah |
|---|---|---|
| LiCoO2(LCO) | 18650型 | 公称容量2.4 Ah |
| LiFePO4(LFP) | 26650型 | 公称容量2.5 Ah |
NMC、LCOは4.2V – 2.75Vで充放電を、LFPは3.6V-2.0Vで充放電を1/10Cで行いました。文献で推奨されているように、温度は正確に30.0±0.1℃で制御しました。(恒温槽Memmert IPP500を使用)
Bio-Logic充放電装置の再現性を試験するため、NMC x 40個、LCO x 20個、LFP x 16個をVMP3(16チャンネル)とBCS-815(8チャンネル)で試験をしました。得られた結果を検証するためオーバークロス測定も行いました。
2-2.ソフトウェアツール
これらの測定はVMP3用のEC-Lab、BCS-815用のBT-Labで利用可能な’’CED’’テクニックで試験を行いました。CEDは“Battery testing”の項目内にあります。
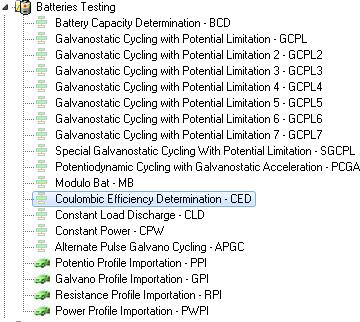
(図1)CEDテクニック選択画面
EM1とEM2に入力された電圧の間を、電流制御で充放電を繰り返します。充電と放電は電流値またはCレートで入力できます。レスト(開回路)は利用できません。(図2)
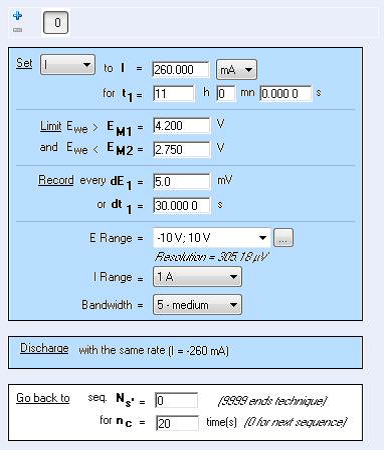
(図2)CEDテクニックのパラメータ設定ウィンドウ
図3では電圧 vs 時間のグラフとCE vs サイクルのグラフを表示しています。
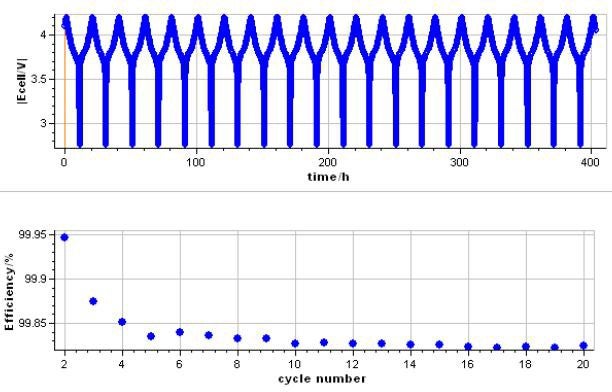
(図3)上:電圧 vs 時間、下:CE vs サイクル
CEDテクニックでは“CED Fit”を利用して、CEのRMSE値を算出できます。(図4参照)
多項式関数とそれに従うRMSE値は測定の最後に自動で計算されます。この解析機能は“Analysis”→“Battery”メニューから利用することができます。
“First hidden point”機能により、最初の測定点は除かれている可能性があります。
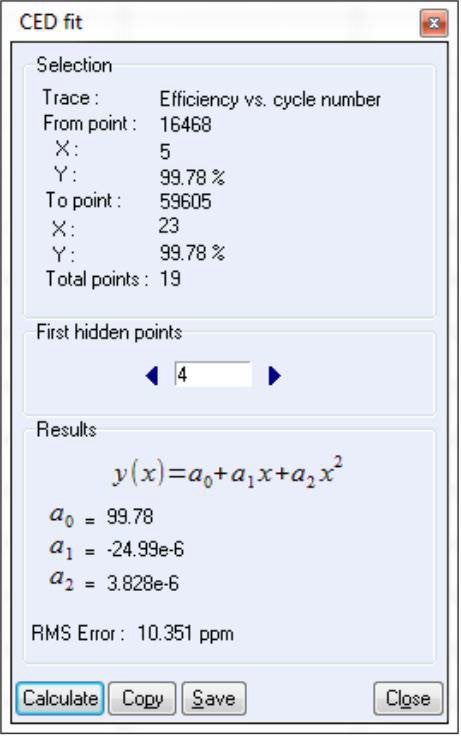
(図4)CED Fitウィンドウ
3.考察
図5ではNMC、LCO、LFP充放電中のセル電圧vs時間を示しています。図6では典型値のCE vsサイクル数の曲線を示しています。フィッティング結果とRMSE値も図6で示されています。
表1はそれぞれの電池におけるVMP3/BCS-815での解析後のRMSE値を示しています。表1からわかるように、RMSE値は電池の技術に依存します。VMP3/BCS-815両機種でも、LCOのRMSE値が一番良い結果でした。
図7ではBio-Logicの装置で評価したそれぞれの電池におけるRMSE値を示しています。LCOの結果は文献[4]に近い結果でした。
3.考察
図5ではNMC、LCO、LFP充放電中のセル電圧vs時間を示しています。図6では典型値のCE vsサイクル数の曲線を示しています。フィッティング結果とRMSE値も図6で示されています。
表1はそれぞれの電池におけるVMP3/BCS-815での解析後のRMSE値を示しています。表1からわかるように、RMSE値は電池の技術に依存します。VMP3/BCS-815両機種でも、LCOのRMSE値が一番良い結果でした。
図7ではBio-Logicの装置で評価したそれぞれの電池におけるRMSE値を示しています。LCOの結果は文献[4]に近い結果でした。
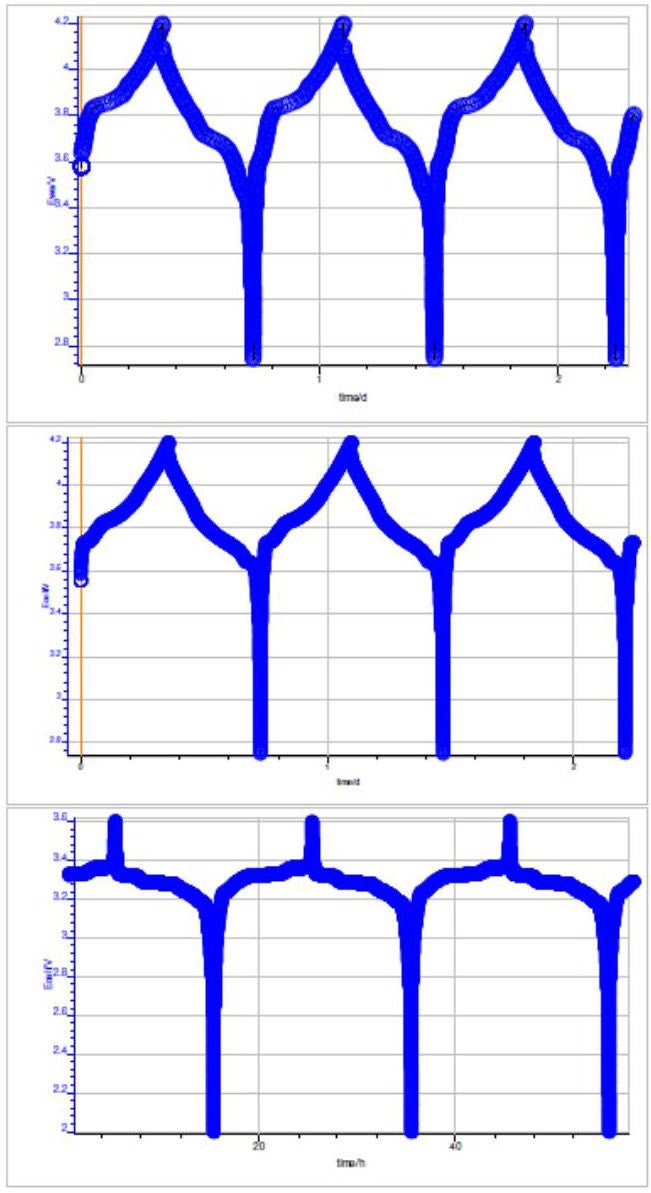
(図5)充放電(10/C)における電圧 vs 時間
上:NMC、中央:LCO、下:LFP
(表1)Bio-Logic装置で測定した各電池における
解析後のRMSEの典型値と最高値

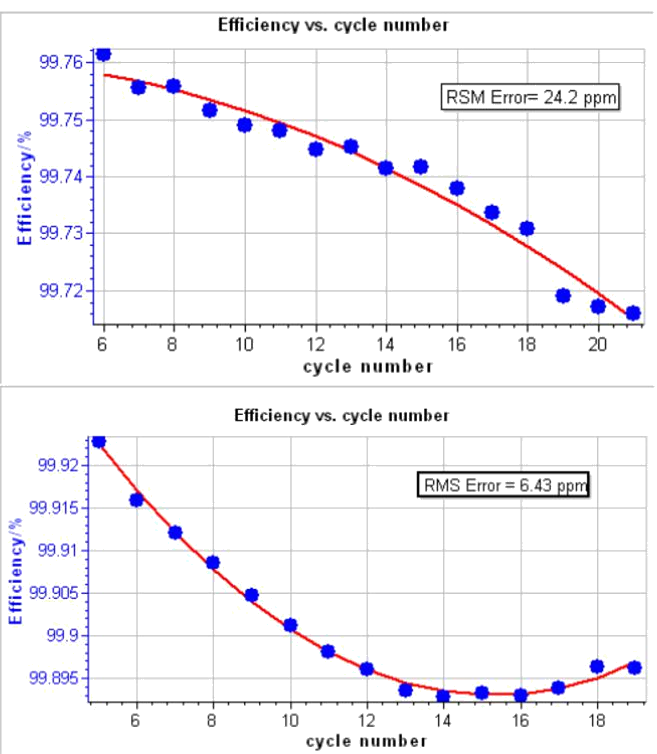
(図6)CE vs サイクル数とフィッティング結果
上:NMCの典型値
下:LCOの典型値
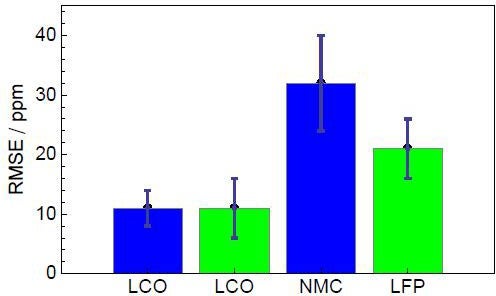
(図7)電池技術の違いにより生じたそれぞれのRMSE値の比較
青:VMP3、緑:BCS-815
この高精度なCE測定はリチウムイオン二次電池の寿命への電解液添加剤、不純物、電極材料、温度の影響を評価できます。また、文献内での測定値からVMP3とBCS-815は典型値11ppmの高精度なCE測定ができます。
4. 参考文献
01) International Vocabulary of metrology. Basic and general concepts an associated terms. JCGM(2008).
02) A. J. Smith, J. C. Burns, S. Trussler, and J. R. Dahn J. Electrochem. Soc., vol. 157, no. 2 (2010) A196.v
03) J. C. Burns, G. Jain, A. J. Smith, K. W. Eberman, E. Scott, J. P. Gardner, and J. R. Dahn J. Electrochem. Soc., vol. 158, no. 3 (2011) A255.
04) T. M. Bond, J. C. Burns, D. A. Stevens, H. M. Dahn, and J. R. Dahn J. Electrochem. Soc., vol. 160, no. 3 (2013) A521.
05) J. C. Burns, A. Kassam, N. N. Sinha, L. E. Downie, L. Solnickova, B. M. Way, and J. R. Dahn J. Electrochem. Soc., vol. 160, no. 9 (2013) A1451.
06) S. R. Li, C. H. Chen, J. Camardese, and J. R. Dahn J. Electrochem. Soc., vol. 160, no. 9 (2013) A1517.
07) J. E. Harlow, D. A. Stevens, J. C. Burns, J. N. Reimers, and J. R. Dahn J. Electrochem. Soc., vol. 160, no. 11 (2013) A2306.
08) R. Petibon, E. C. Henry, J. C. Burns, N. N. Sinha, and J. R. Dahn J. Electrochem. Soc., vol. 161, no. 1 (2014) A66.
09) “Nomenclature, symbols and definitions in electrochemical engineering”, Pure Appl. Chem., vol. 85 (1993).
10) International vocabulary of metrology – Basic and general concepts and associated terms. Joint Committee for Guides in metrology (2012).
5.付録:誤差の計算
5-1. dQ誤差の計算
一定電流下で、電気量は下記のように定義されます。

Iは印加電流、teは充放電時間です。もしdIとdtが不確かまたはIとtの測定で誤差がある場合、Qの計算における誤差は下記のように表されます。

dIは電流測定精度に一致します。測定時間の精度であるdtは電池電圧と温度の関数(te=f(V,T))で、電圧リミットの検出精度に依存します。そのためdtは下記のように表わせます。
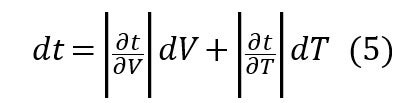
(4)と(5)を組み合わせると下記の式が得られます。
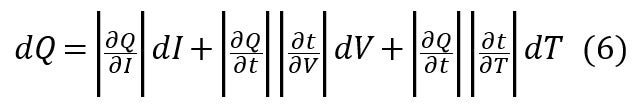
∂t/∂Vは時間に対する電圧の関数の傾きの逆数で、dVは電圧測定に関するエラーで、dTは温度測定のエラー∂t/∂Tは温度による充放電時間の変化です。下記の式よりこの値を算出できます。
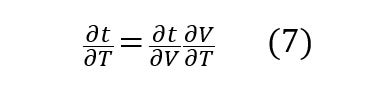
∂V/∂Tは電圧の温度ドリフトです。これは電池の性能によります。そのため下記の式が導けます。
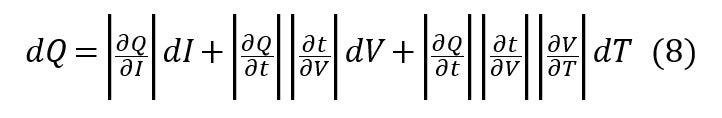
5-2. dΦQ誤差の計算
上記で述べたように、クーロン効率(ΦQまたはCE)は下記の式で表せます。
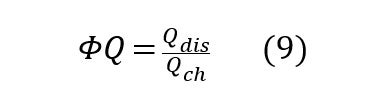
そのため、ΦQに関連する誤差は下記のように表されます。
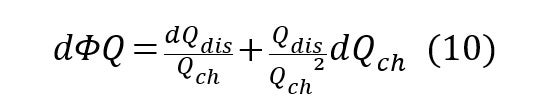
※【EC-Labユーザー向け】本アプリケーションノートのデータは下記フォルダに保存しています。
C:\Users\xxx\Documents\EC-Lab\Data\Samples\Battery\ AN53_LCO_LIS-18650_CED_CA1
2018年07月改訂
電気化学測定装置のお取り扱いページへ
お問い合わせ先
株式会社東陽テクニカ 脱炭素・エネルギー計測部
