等価回路における改良型インダクタンス素子(La)
I- はじめに
インピーダンスのナイキスト線図に半円が示されていて、その中心がX軸上ではなく実軸より下にある場合などは、コンデンサの代わりにコンスタント・フェーズ・エレメント(CPE)を使用する方が便利です。
コンデンサCとCPE Qの差異は、CPEのインピーダンスの式に追加のパラメータaが含まれている点です。
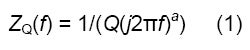
一方、コンデンサのインピーダンスの式は、次のとおりです。
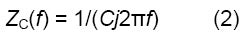
Cはコンデンサ[F]、QはCPE[F s(a-1)]の値です。(0<a≦1)
a = 1の場合は、Z(f)Q = Z(f)Cである点に注意することが重要です。CPEは物理的なサンプルの表面の粗さの影響として解釈され、これはコンデンサの不均一性と関連付けられます。
同様に、改良型インダクタンスLaを使用すると、ナイキスト線図内の通常の挙動ではないインダクタンスの軌跡を表現することができます。インダクタンスのインピーダンスの式は、次のとおりです。
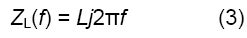
改良型インダクタンスLaのインピーダンスの式は、次のとおりです。
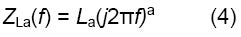
Lはインクダンス[H]、Laは改良型インクダンス[H s(a-1)]の値です。(0<a≦1)
この場合も、a = 1であれば、ZLa(f) = ZL(f)です。
本項では、改良型インダクタンス素子によりインピーダンスデータをうまく近似できる実例を紹介します。
II– リチウムイオン電池における高周波インダクタンス
図1に、容量60Ahおよび公称電圧3.2VのLiPF6リチウムイオン電池のインピーダンスのナイキスト線図を示します。電池への接続ケーブルに大きく起因すると思われるインダクタンスの挙動は、高周波(f>22 Hz)で見られます。本挙動は、皮相抵抗の低い電池などのセルで見かけることがよくあります。図1で線形最小二乗近似によって示されているように、これらの高周波データ点は、X軸に垂直でない直線上にあります。そのため、本挙動を基本的なインダクタンスで表すことはできません。
図1に示したデータを近似するために選択した等価回路を、図2に示します。
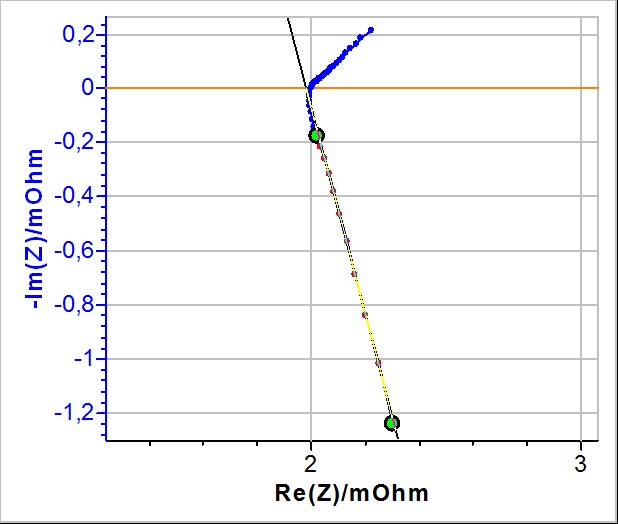
図1: LiPF6電池のナイキスト・インピーダンス線図(周波数∈[0.1 , 2000] Hz)
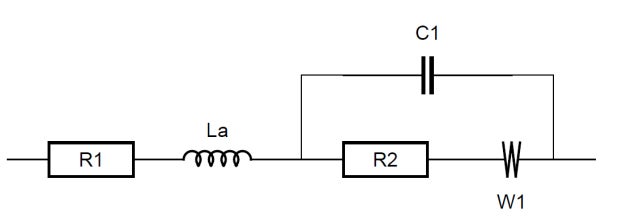
図2: 改良型インダクタンスが直列接続されている
Rundlesの等価回路
これは、インダクタンスLaが直列接続されているRandlesの回路です。基本的なLは、インダクタンスLaの特殊ケースです。前述のように、a=1であればLa≡Lです。R1は電池の内部抵抗、C1は二重層の容量、R2は電荷移動抵抗、W(Warburgコンポーネント)は半無限拡散に関連付けられています。 図2に示す基本的なインダクタンスを含む等価回路を使用して得られる近似曲線を、図3に示します。
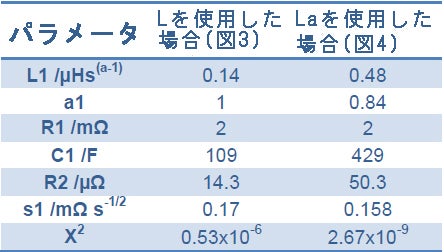
図4も同じ結果を示していますが、図4の場合は改良型インダクタンスLaを使用しています。2つの近似結果、すなわちパラメータ値とχ2値の比較を、表1に示します。(χ2値は近似の良さを推定した値[1])
図3に示したように、インダクタンスLの代わりに改良型インダクタンスLaを使用すると、インピーダンスの垂直でない高周波部を近似することができます。Randlesの等価回路と直列接続されている改良型インダクタンスを使用し、図1の電池インピーダンスを近似した結果を、図4に示します。この場合、χ2は小さいため、基本的なインダクタンスが含まれる等価回路を使用して得られるχ2ファクタより優れています(表1を参照)。また、表1では、C1、R2、およびW1の値が異なっています。それは、改良型インダクタンスを使用すると、パラメータの決定をより良くできることを示しています。
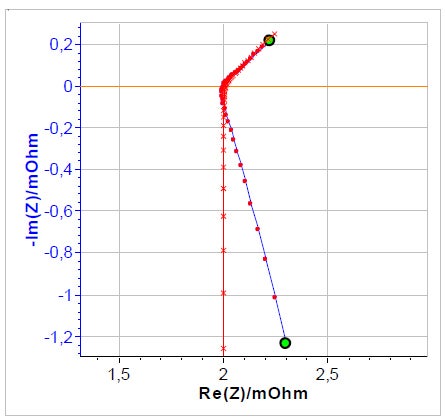
図3: 等価回路L1+R1+C1/(R2+W1)を使用して図1のインピーダンス図を近似した結果
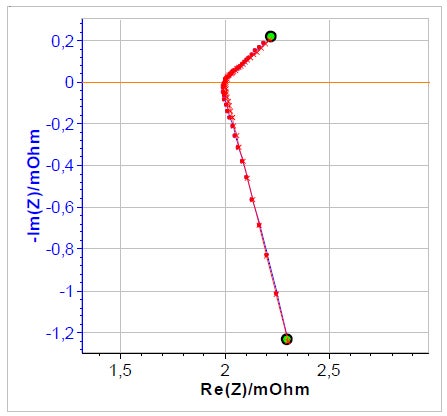
図4: 等価回路La1+R1+C1/(R2+W1)を使用して図1のグラフを近似した結果
表1: 図3および図4で使用した等価回路のパラメータ値
III-自然腐食金属の低周波誘導挙動
コンポーネントLaを使用できる例としては、酸性溶液内の金属腐食という系もあります。その場合、還元反応はプロトン還元であり、Volmer-Heyrovskýメカニズムに従って、吸着ステップが含まれます[2-4]。図5は、0.5mol L-1 H2SO4に浸漬された部分的に塗装されたZnサンプルで得られたインピーダンスプロットと、図6で示す等価回路を使用した近似曲線を示しています。
この等価回路の場合、Q1/R1は図5の比較的大きな半円形(サンプルの被膜部に起因する可能性がある)、Q2/R2は誘導的半円形(金属の粗い表面における吸着過程に起因する)、Q3/R3は第3の半円形(地金に起因する可能性がある)に関連付けられています。
この例で使用した溶液は完全なイオン導電体ではなく、その抵抗(約1Ω)は無視できると考えました。
インピーダンスプロットは、Volmer-Heyrovskýの化学的脱着メカニズムを考慮して解釈することもできます([2])。
表3で示す近似結果において、要素Q2/R2は誘導ループに対応しており、負の値を持ちます。負の値の取り扱いおよび解釈は、測定者にとって困難な場合もあります。そのような場合は、要素が正の値を持つ等価回路を使用することができます。図6の回路R1+Q2/R2を図7のR1/(R2+La2)に置き換えることで、正の値で表現できます。
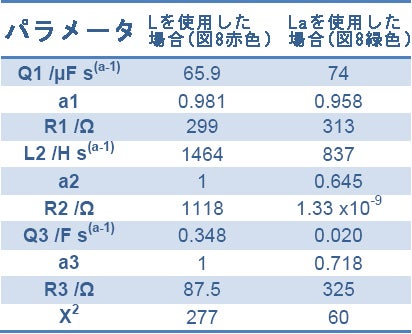
図8の青色の曲線は実験データ、赤色の曲線は基本的なインダクタンス(a2 = 1)を含む等価回路(図7)を使用して得られた近似曲線です。緑色の曲線は改良型インダクタンスを含む等価回路(図7)を使用して得られた近似曲線を示しています。
表3に見られるように、等価回路の要素はすべて、正の値を持つようになっています。最良の等価回路を選択するという観点から見ると、赤色の曲線は緑色の曲線に比べて実データに対する近似が良くありませんが、それは改良型インダクタンスによって近似が改善されていることを示しています(図8の挿入部分を参照)。近似の良さは表3で示すχ2の値によって確認できます。
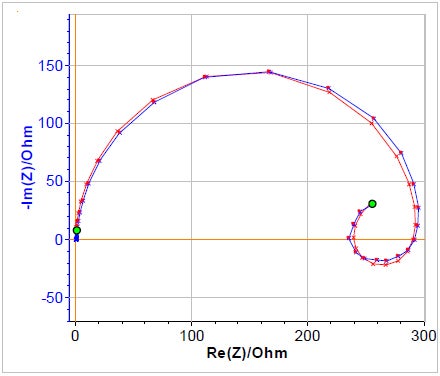
図5: 青色: 0.5mol L-1H2SO4に浸漬された部分的被膜のZnサンプルのインピーダンスのナイキスト線図(周波数∈[10x10-3 , 200x103] Hz)
赤色:Q1/(R1+Q2/R2+Q3/R3)を使用した近似曲線
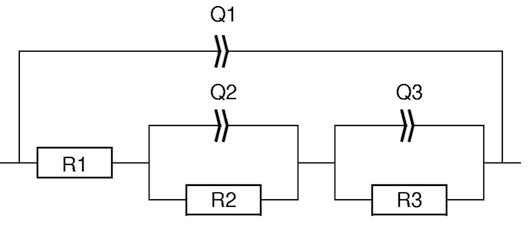
図6: 図5で使用されている等価回路
表2: 図5で使用した等価回路のパラメータ値
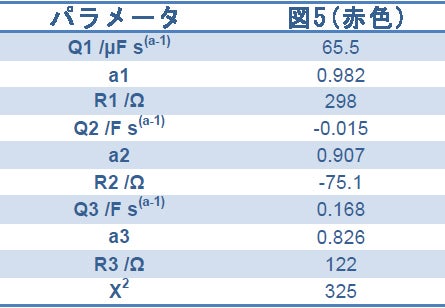
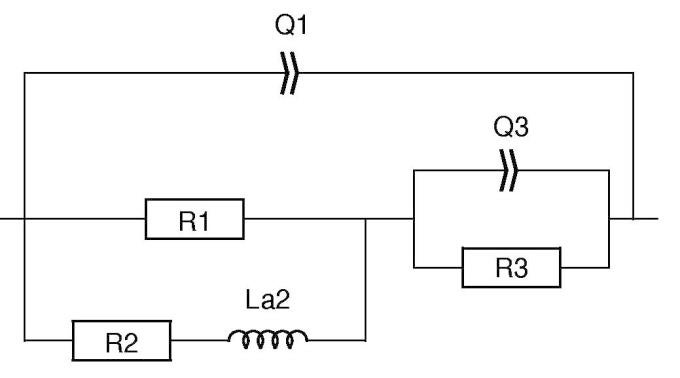
図7: 図8で使用されている等価回路
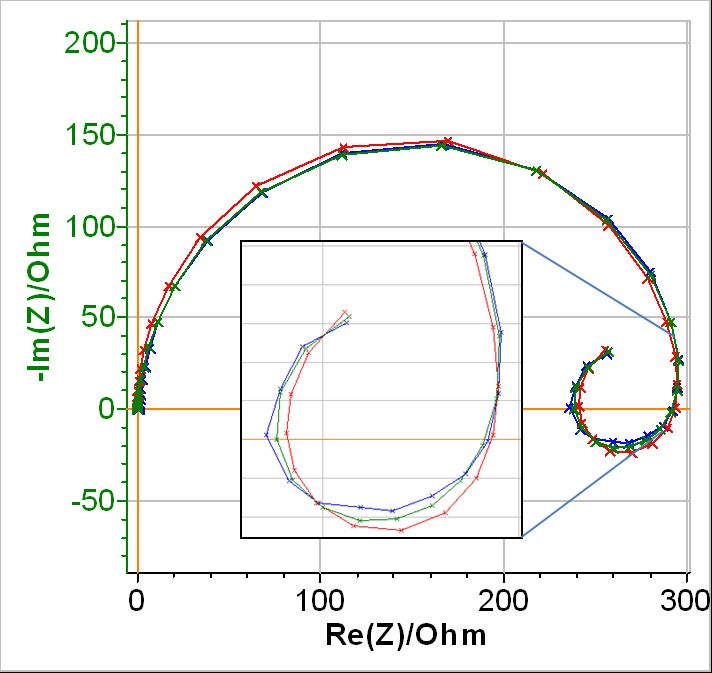
図8:青色: 0.5mol L-1 H2SO4に浸漬された部分的被膜のZnサンプルのインピーダンスのナイキスト線図。
近似曲線は赤色: Q1/(R1/(R2+L2)+Q3/R3)、緑色: Q1/(R1/(R2+La2)+Q3/R3)を使用
表3: 図8で使用した等価回路のパラメータ値
IV- 結論
新しい素子Laは、改良型のインダクタンス素子です。これを使用すると、高周波での通常の挙動ではない配線のインダクタンス(主に電池で見られる)、または低周波での不均一な吸着メカニズム(主に腐食で見られる)に関連するインピーダンス特性を近似することができます。
参考文献:
- EC-Lab® User’s Manual p. 113
- Interactive Faradaic Impedance Library, http://bio-logic.info/potentiostat/notesifil.html
- M. Keddam, Thèse, Paris, 1968, no. AO2192.
- J.-P. Diard, P. Landaud, B. Le Gorrec, C. Montella, J. Electroanal.Chem., 255 (1988) 1.
付録
1) 図5の誘導ループをR/QではなくR/Cで近似できる(すなわちa2が1に等しい)場合は、R+Lで十分であり、R+Laが不必要であることは注目に値します。
2) さらに、等価回路に関する見識を広める場合、aQ = -aLa、Q = 1/Laで、aQが素子Qのaパラメータ、aLaが素子Laの同パラメータの場合、ZQ(f) = ZLa(f)であることも注目に値します。
式4でaを-aQに置き換えると、次のようになります。
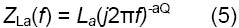
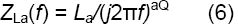
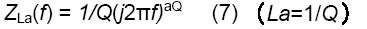
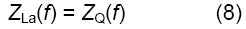
最後に、C、L、Q、およびLa素子のインピーダンスはすべて、次の一般式の1つです。
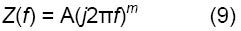
Aは該当コンポーネントの値で、m ∈[-1,0[∪]0,1]。
m= 0の場合、インピーダンスZはただの抵抗です。
データ
図1: ECLab\v10.xx\Data\Samples\Battery\AN42_battery.mpr
図5: ECLab\v10.xx\Data\Samples\Corrosion\AN42_coating.mpr
お問い合わせ
株式会社東陽テクニカ 理化学計測部