IRドロップ ③-ZIRテクニックの適切な使い方
IRドロップ③-ZIRテクニックの適切な使い方
本書はBiologic社が発行するApplication note #29を2020年9月において翻訳したものです。 今後、原文が改訂され、内容が変更された場合には、改訂後の原文の内容を優先いたします。
1.序文
Application Note#28で示した通り、EIS測定は電解液抵抗RΩ(または、未補償抵抗Ru)を求める優れた手法です。RΩは、作用電極と参照電極の間の電解液抵抗だけでなく、配線などといった作用電極自体に寄与するすべての抵抗値の和として定義されます。
EC-Labの解析テクニックZFitを用いることでRΩを計算することができます。ZFitでは等価回路がわかっていることが前提となっていますが、明らかとなっていない場合もあります。
本ノートの目的はインピーダンス測定のテクニック(ZIR)を用いてIRドロップの決定、補正を行い、ZFitを用いることなくRΩの値を求める方法を述べることです。また、本ノートの一部では、いくつかの測定系におけるこの手法の制限についても言及します。
2.ZIRテクニックとは
インピーダンス測定によってIRドロップを決定、補正するテクニック(ZIR)はPEISテクニックと大変似通っていますが、このテクニックではEIS測定は一つの周波数fZIRのみで行われます。そのため、下記の関係式が成り立ちます。
RΩ=ReZ(fZIR)
このテクニックでは、電解液の抵抗は高周波領域の一つの周波数でのみEIS測定を行います。周波数は図1に示すように、デフォルトでは100kHzとなっています。
ZIRテクニックはEC-Lab、EC-Lab expressソフトで使用でき、EC-Lab expressの場合には、電圧制御モードと電流制御モード(ソフト上ではそれぞれPZIR、GZIRと表記されます)があります。

(図1)ZIRテクニックのパラメータ設定画面
3.高周波におけるインピーダンス測定の等価回路
3-1.インピーダンス測定の等価回路
インピーダンス測定における等価回路を図2に示します。
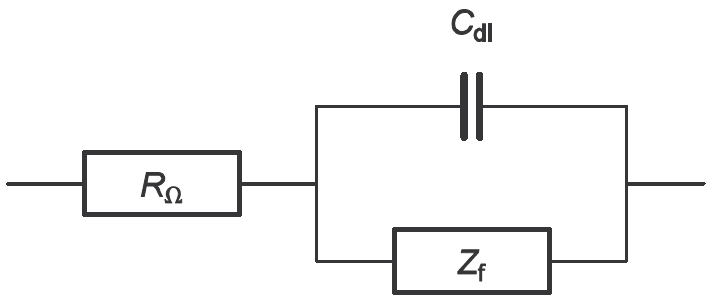
(図2)インピーダンス測定の等価回路。Cdlは電気二重層容量を表します。
ファラデーインピーダンスZfの等価回路は電気化学的な反応によって決まります。
例として、ある酸化還元反応の等価回路を図3に示します。
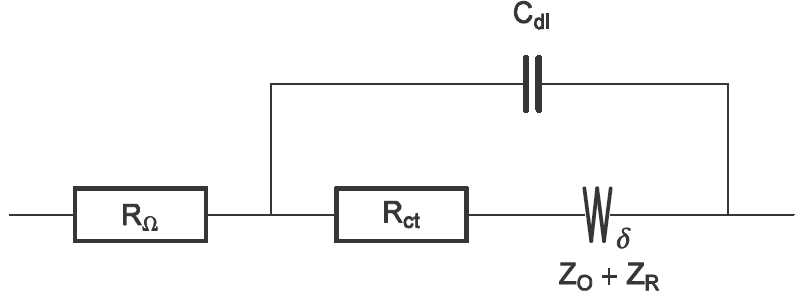
(図3)ある酸化還元反応の等価回路
3-2.高周波におけるインピーダンス測定の等価回路
図4に示すように、ある電気化学反応の高周波における等価回路を考えましょう。Zfは以下の式で表されます。
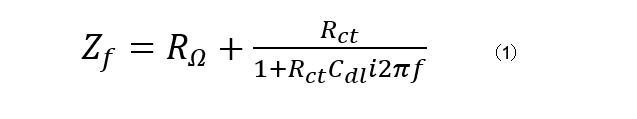
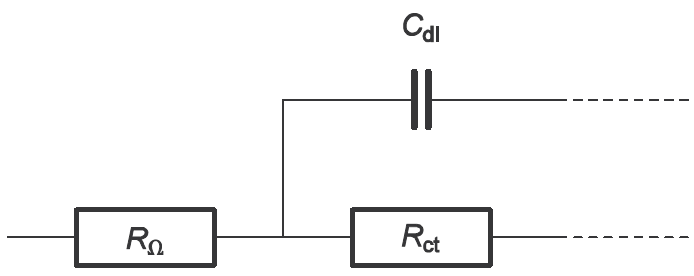
(図4)LSVの設定画面
Zfの実部は以下の式で表されます。
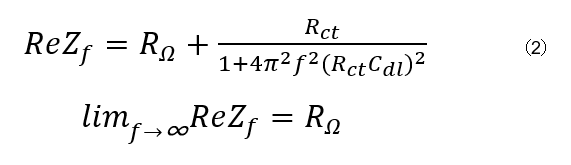
この式からわかるように、インピーダンスZfの実部は、周波数が無限大に近づくにつれてRΩに近づきます。(図5)
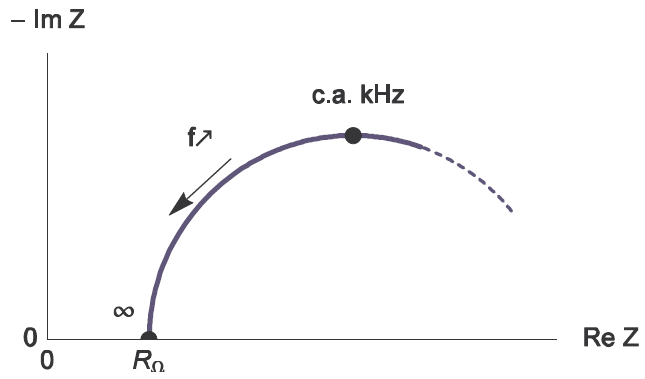
(図5)インピーダンスの等価回路における高周波でのナイキスト線図
4.最も単純な場合におけるRΩの測定
式(2)から、Zf実部は周波数に応じて変化することがわかります。測定の相対誤差ε(f)は以下のように表すことができます。
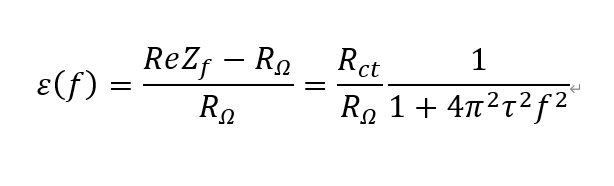
様々なRct/RΩの比における相対誤差の変化を図6に示します。
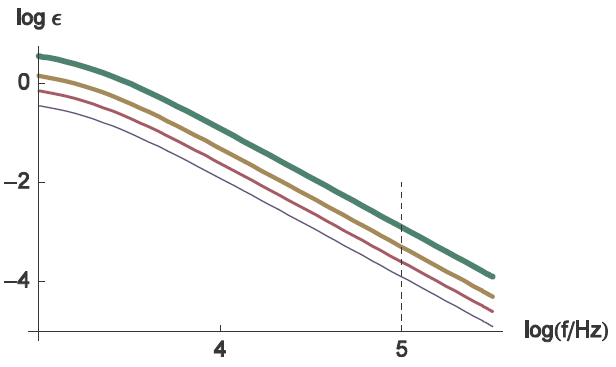
(図6)RΩの相対誤差の周波数変化
Rct/RΩ = 0.5, 1, 2, 2.5、τ = RctCdl = 10-4 s
(線の太さはRct/RΩの比が大きくなるに従って太くしています。)
5.直列にインダクタンスがつながった場合のRΩ測定
5-1.直列につながったインダクタンス
電気化学系(例えば電池など)によっては、高周波でインダクタンスの挙動が見られることがあります。このような系での等価回路は図7のように表されます。インダクタンスはケーブルとの接続や電池ホルダーに関係します。
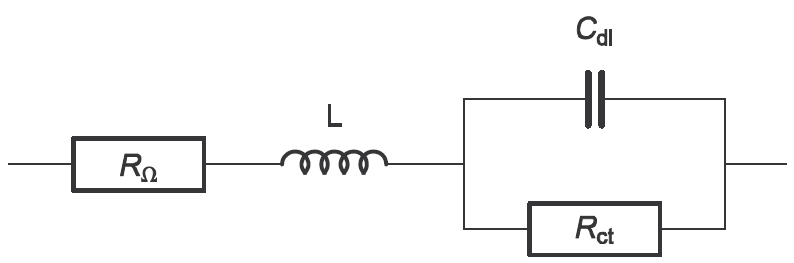
(図7)直列のインダクタンスを想定したファラデーインピーダンスの高周波数での等価回路
図7のインピーダンスは以下の式で表されます。
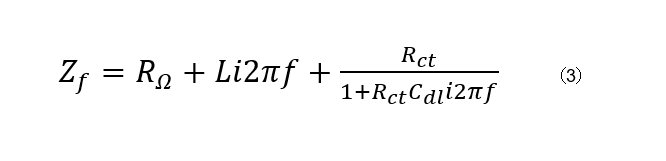
Lの値によってインピーダンスのグラフは変化します。図8にインダクタンスが直列につながっているときの様々なインピーダンスグラフの形状の例を示します。図8に示された曲線はEC-LabのZSimやBio-Logicのウェブサイトで利用できる等価回路ライブラリから作成できます。
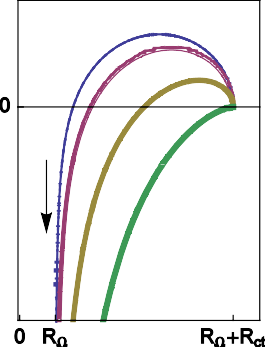
(図8)R+L+(R/C)回路のインピーダンスのナイキスト線図(図7(式(3)))
RΩ = 0.2Ω、Rct = 1Ω、Cdl = 10-4F、L = 10-5, 5 x 10-5, 10-4H
線の太さはLの値が大きくなるに従って太くなっています。
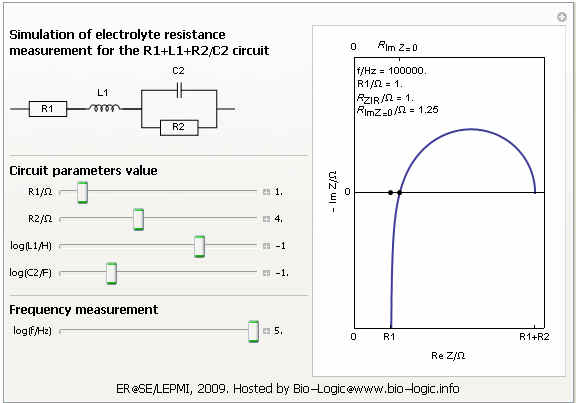
(図9)Bio-Logicのウェブサイトで利用可能な等価回路ライブラリ
幸運なことに、インピーダンスの実部はインダクタンスLを追加した際(式(3))でも前の例(最も単純な場合におけるRΩの測定)と比べてあまり変わりません。そのため、R+L+(R/C)の回路におけるZfの実部はやはり式(2)で表されます。さらに、Rにおける相対誤差の曲線はインダクタンス(L)の値には依存しません。そのため、図10に示す値は図6で与えられた値と同じになります。
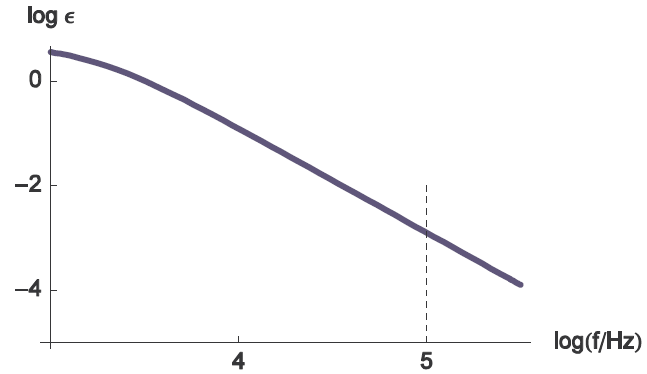
(図10)RΩ測定における相対誤差の周波数変化。パラメータの値は図8と同様
5-2.直列につながった(R/L)回路
高周波の挙動は直列のインダクタンスの挙動となることもありますが、場合によっては直列の(R/L)回路となることもあります。この回路のインピーダンスは以下の式で表されます。
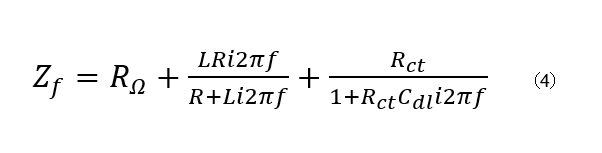
式(4)の実部は以下の式で表されます。
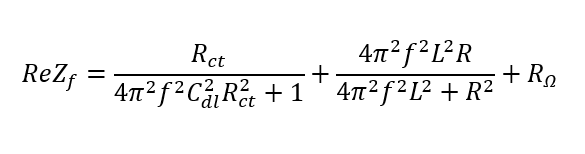
この値はLとRに依存します。
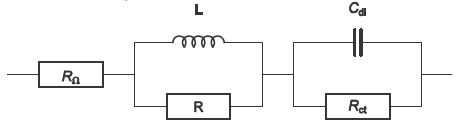
(図11)直列の(R/L)回路を考慮した高周波側でのファラデーインピーダンスの等価回路
図12にR+(R/L)+(R/C)の系から得られるインピーダンスのナイキスト線図を示します。違う形状のナイキスト線図が得られていることに注意して下さい。このようなナイキスト線図は電池の系で得られる場合があります。参考文献[6]で鉛蓄電池の場合や図13でリチウムイオン電池の場合を例として記載します。
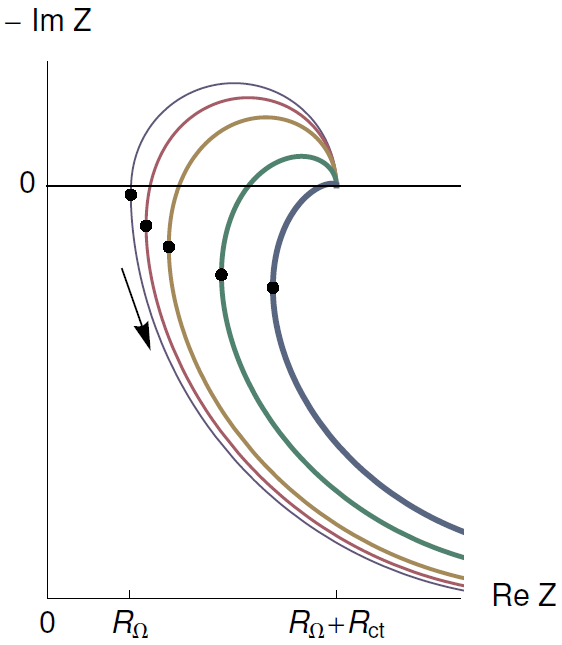
(図12)R+(R/L)+(R/C)の回路に対するインピーダンスのナイキスト線図(図11(式(4)))
RΩ = 0.2Ω、Rct = 5Ω、R = 2Ω、Cdl = 10-4F、L = 10-7, 2 x 10-6, 5 x 10-6, 1.3 x 10-5, 2.3 x 10-5H
線の太さはLの値が大きくなるに従って太くなっています。
先に述べたように、図12に示される曲線はEC-LabのZSimやBio-Logicのウェブサイトの等価回路ライブラリから得ることができます。
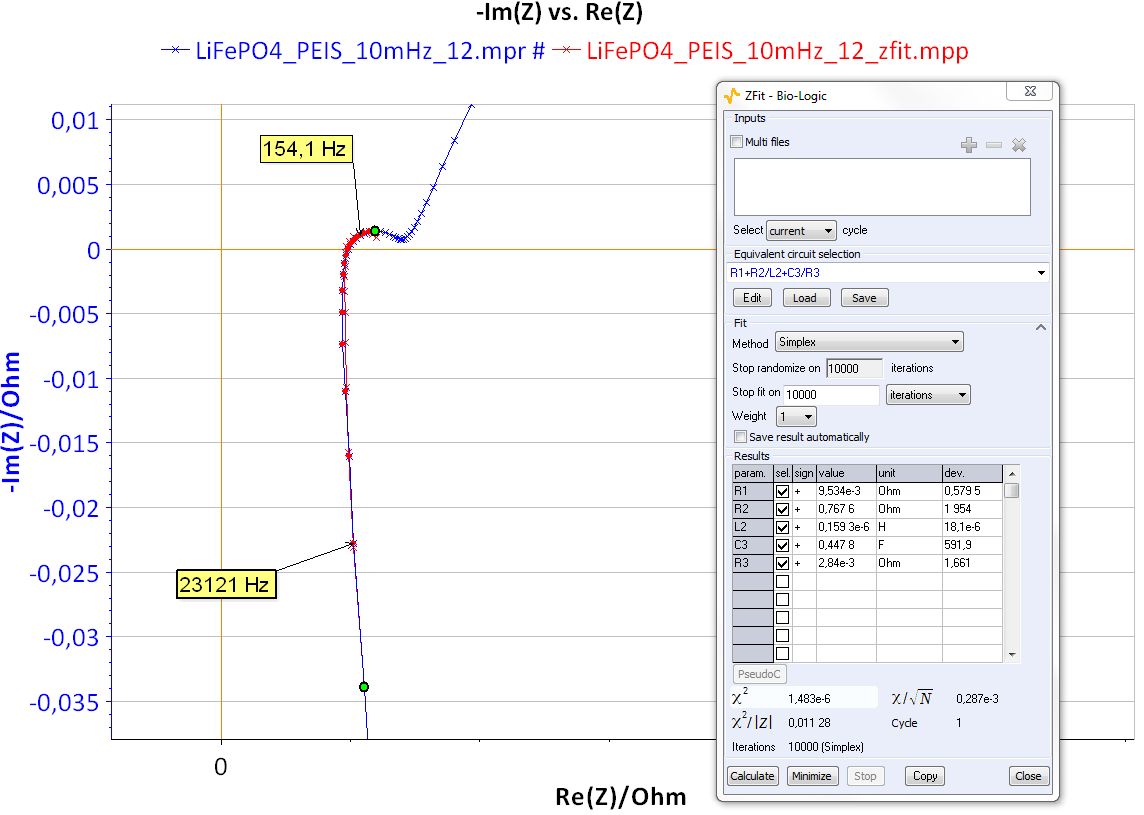
(図13)リチウムイオン電池で得られたナイキスト線図とZFitによる解析結果
RΩの相対誤差の周波数変化を図14に示します。この相対誤差は周波数の増加に伴って単調に減少はしていません。この場合、相対誤差の最小値はインピーダンスの実部が最小となる周波数、すなわち、図12においてドットで強調された周波数に対応します。
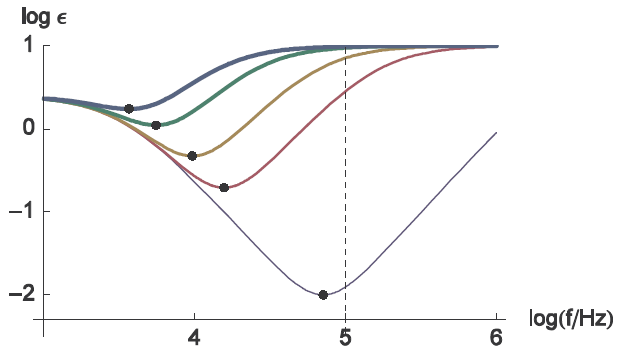
(図14)RΩ測定における測定誤差の周波数に対する変化
各パラメータの値は図12で使用した値と同じです。
また、ドットはRΩ測定における相対誤差の最小値を示します。
6.まとめ
ZIRテクニックを使うことで、ZFitを用いることなくRΩを決定することができます。このZIRテクニックは測定系がインダクタンスの挙動を示さなければ体系的に用いることができます。しかし、測定系がインダクタンスLを含む場合、ZIRテクニックを用いる前にいくつか注意を払わなければなりません。この場合、ZIRテクニックのおける合理的な周波数を決定するためには、事前にインピーダンス測定を行い、図11の等価回路によるZFit解析を行う必要があります。
本ノートではRΩの値を決定する方法を主に述べましたが、ZIRテクニックはIRドロップの補正にも用いられます。そのためには、補正値を用いるテクニックの前にZIRテクニックを配置する必要があります。

(図15)関連する実験でIRドロップを補正する設定方法
7. 参考文献
1) Bio-Logic Application Note #28
2) Electrochemical methods. Fundamentalsand applications, A. J. Bard, L. R. Faulkner, ed. Wiley (Hoboken), 2001
3) Bio-Logic Application Note #27
4) EC-Lab Software Techniques and Applications Manual
5) Huet, F., Nogueira, R. P., Torcheux, L.,and Lailler, P. Simultaneous real-time measurements of potential and highfrequencyresistance of a lab cell. J. PowerSources 113 (2003), 414–421.
電気化学測定装置のお取り扱いページへ
お問い合わせ先
株式会社東陽テクニカ 脱炭素・エネルギー計測部
