ステップ電圧制御電気化学インピーダンス測定(SPEIS)と自動連続ZFit解析
ステップ電圧制御電気化学インピーダンス測定(SPEIS)と
自動連続ZFit解析
本内容はBiologic社が発行するApplication note #18を2020年7月時点で翻訳したものです。
今後、原文が改訂され、内容が変更された場合には、改訂後の原文の内容を優先いたします。
1.導入
EC-Lab®およびEC-Lab®Expressでは、SPEIS(Staircase Potentio Electrochemical Impedance Spectroscopy)テクニックを使用して、電位ステップ掃引中に連続でインピーダンス測定を行うことが可能です。
このテクニックを使用することにより、各電位ステップにおけるインピーダンス測定を自動で実行することができます。この技術の主な使用目的は、定常分極曲線に沿った電気化学の反応速度を調べることです。
電流制御であるSGEISテクニックを用いた際にも同様の測定を行うことが出来ます。
2.実験
測定はEC-Lab®のSPEISテクニックを用いて実施しています。
設定は図1に示します。
試料としてBio-Logic Test Box3の回路を使用しました。
このテクニックを使用することで、直流電圧をスイープする初期電位、最終電位、ステップ数を設定することが出来ます。2つ目のブロックではEIS測定行う前の待機時間を設定します。3つ目のブロックでは周波数範囲などのEIS測定の設定を行います。
EISの設定は次の通りです。
100kHzから50mHzまでの周波数掃引し、1decadeあたり6ポイントで記録を行います。振幅は5mVに設定しています。Pwは1に設定し、各周波数測定後に実験系が定常状態に戻るようにしました。
Naは2に設定し、平均値を記録するようにしています。
なお、上記実験を行うには約2時間を要します。
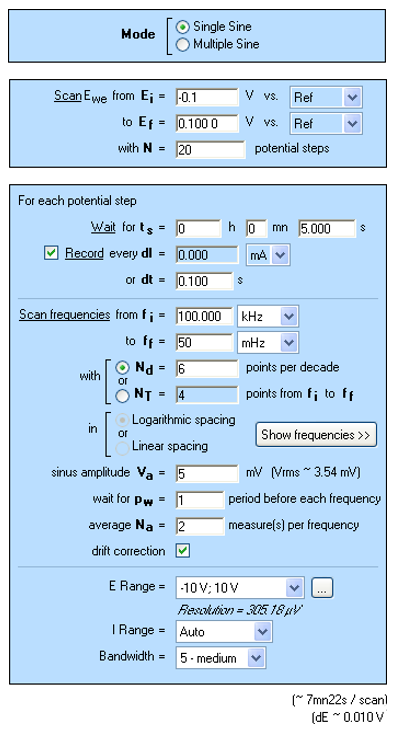
図1 SPEISテクニックのパラメータウインドウ
2-1.ダイオードのパラメーター決定
Bio-Logic test Box3を用いて-0.2V~0.2Vの範囲でLSV[リニアスキャンボルタンメトリー]を行いました。
その結果を図2に記載します。
*参照ファイルではCVテクニックを用いてLSV測定を行っています。
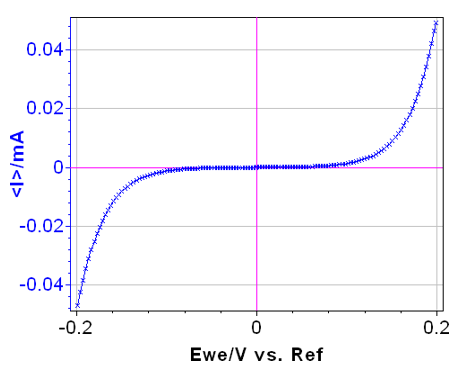
図2 I vs Eweの定常分極曲線
この回路は2つの半導体ダイオード〔1〕で構成されており非線形の特性を示し、Butler-Volmerの関係式を模倣しています。この回路(#2)の電流電圧特性は以下の関係式で表されます。
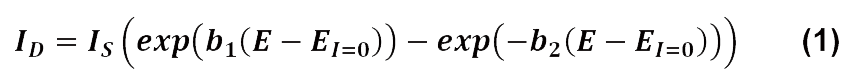
または、Sternの関係式に変換すると下記の式となります。
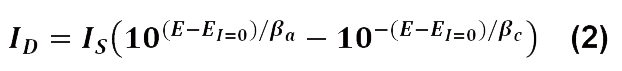
Is、βa、βc、およびEI=0は、EC-Lab®ソフトウェアのTafel Fit解析を使用し算出できます。(図3参照)
以下の値が得られました。
IS=2.7×10-8A
βa=0.062V
βc=0.059V
EI=0=-0.003V
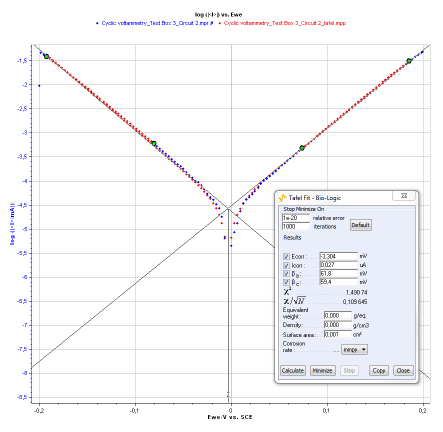
図3 Tafel Fit Analysis
2-2.SPEIS測定
SPEIS測定テクニックを使用し、-0.1V~0.1Vの範囲を電位ステップ10mVでEIS測定を行いました。測定結果を図4に示します。
Test Box3(#2)の定常分極曲線より、インピーダンス測定の電位はアノード部とカソード部の曲線に近いため2つのそれぞれのグループに分けられます。
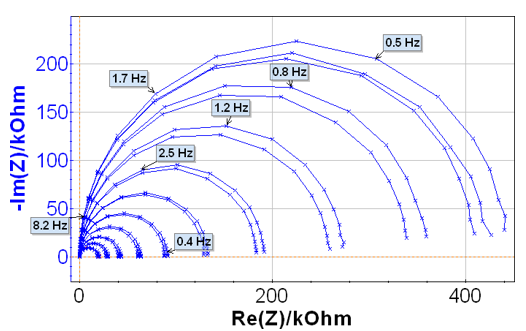
図4 定常分極曲線に沿ったナイキストプロット
2-3.自動等価回路フィッティング
EC-Lab®に搭載されているZFitを使用することでインピーダンス測定結果の等価回路フィッティングを行うことが出来ます。
また、ZFitを使用して等価回路フィッティングを行う際に、等価回路が同一の場合は複数の測定結果を同時に解析することが可能です(図5参照)。設定パラメータを図6に示します。
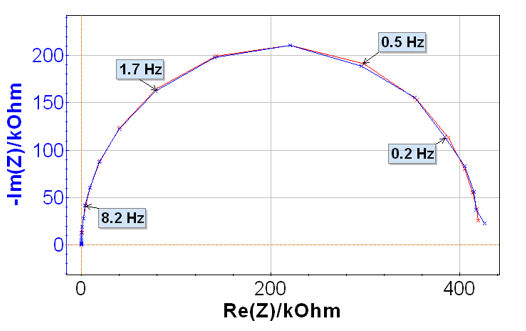
図5 ZFit後のナイキストプロット
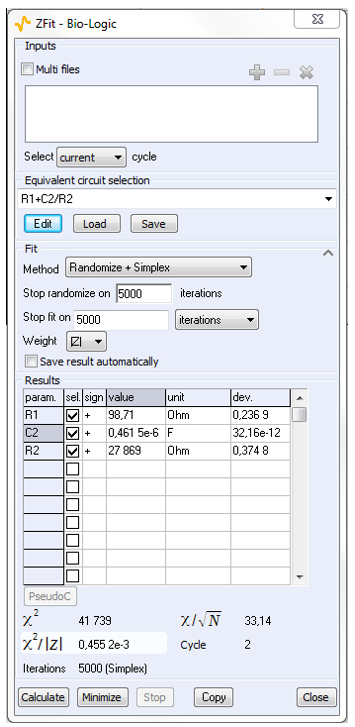
図6 ZFitウインドウ
フィッティングに使用した等価回路を図7に示します。この回路はコンデンサC2と並列の抵抗R1と並列の抵抗R2で構成されています。R1の値は、電位範囲に沿って一定であり、100Ω付近であることが分かります。しかしながら、非線形性のために、この回路の他の素子については同じではありません。図4から分かるように、この非線形回路のインピーダンスは作用電極電位Eweの値に依存します。
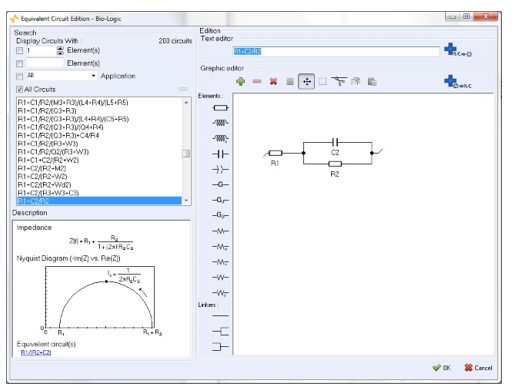
図7 ZFitにおける等価回路の選択
ZFitツールを使用すると、各電位のインピーダンス結果を解析し、R2およびC2値の連続した値を作用電極電位の関数としてプロットすることができます。この結果を図8に示します。R1の値は電位掃引範囲においてほぼ100Ωであったため、この図には記載されていません。
また、C2(約0.46×10-6F)の値は、ポテンシャル範囲に沿って一定です。図8では電位に依存してR2が変化しているのが確認できます。
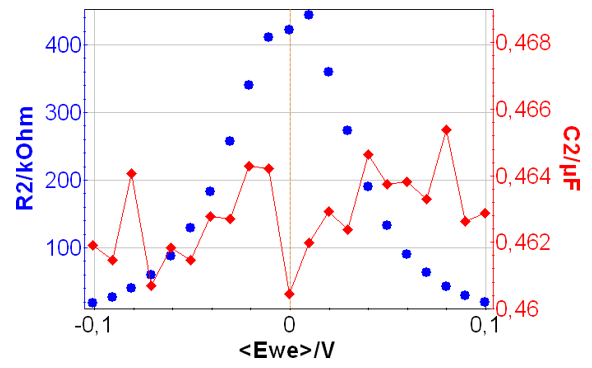
図8 R2、C2の電位依存性
2-4.回路パラメータの決定
ZFitを使用して得られたR2の変化と、図8で示されている21個のナイキスト図を見てみましょう。低周波領域での入力信号におけるTest Box3(#3)の回路#2の動的特性は定常状態の式(1)で表すことが出来ます。
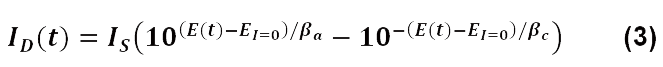
したがって、この回路における電荷移動抵抗は次のように与えられます。
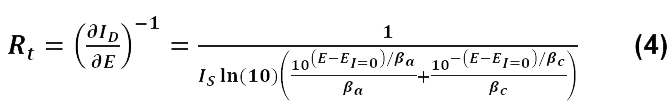
図7に示されている等価回路と、R2と比較してR1が無視できることを考えると、(4)式は次のように書くことが出来ます。
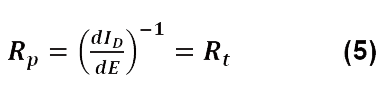
ここではR2=Rpです。 Mathematicaソフトウェアの非線形回帰などのフィッティング手順を使用して、Is,βa,βc ,EI=0の値を決定することが可能です。結果を図9に示します。
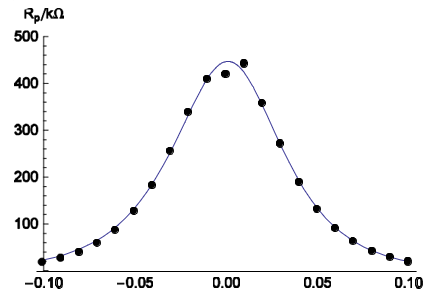
図9 :Is=2.97x10-8A、βa=0.059V、βc=0.064VおよびEI=0>=0.0032Vについて
計算した図8(点)および理論曲線(実線)から得られた実験データの比較
これらの結果から、動的な状態(実験結果)と定常状態(シュミレーション結果)が一致することが分かりました。これはこの系において定常状態の関係式が動的な状態を解析する際にも使用することが出来ることを表しています。
3.非定常電気化学系の自動ZFit
腐食電極や電池など時間と共に変化する非定常状態の系を測定する事があります。自動ZFitは経時変化する系の解析にも使用することが出来ます。
系の時間による変化の例を図10に示します。これは酸化中のNaBH4のプラトー拡散におけるインピーダンスを16回連続で測定した結果です。〔5-7〕
![]()
全てのナイキスト線図は二つのRC並列回路からなっていることが分かります。
PEISテクニックを用いてEIS測定を行い、同様の測定を15回繰り返しました。設定パラメータを図11に示します。
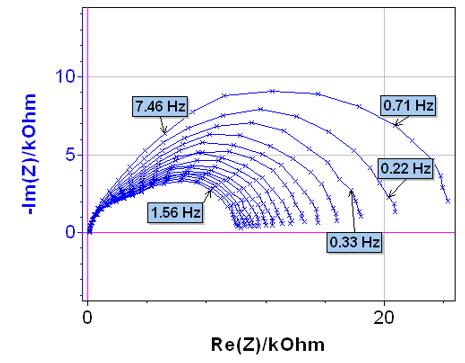
図10 酸化中のNaBH4のRDE(金電極)による
プラトー拡散のインピーダンス
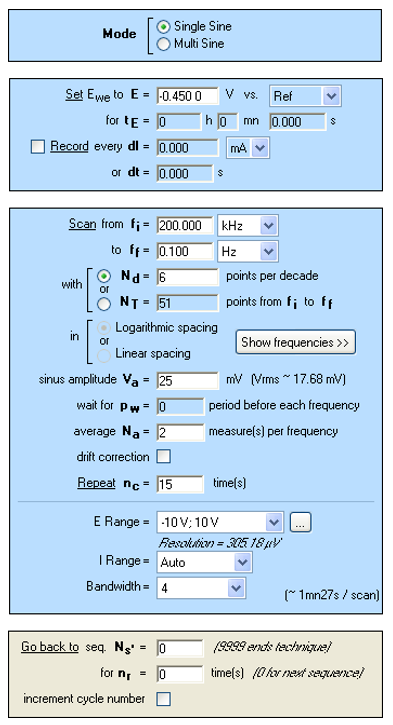
図11 PEISのパラメータ設定ウインドウ
経時変化する系のナイキストプロットの解析にはZFitを使用することが出来ます。図10のナイキストプロットの形状から等価回路はR1+C2/(R2+Wd2)を選択しました(図12)。フィッティングの例を図13に示します。 次いで、ZFitを使用して、R1、C2、R2、Rd2またはtd2の変化をサイクル数の関数として自動的にプロットすることが可能です。例として、R2、Rd2およびC2の変化を図14に示します。 これにより、腐食電極または電池のような非定常の系の連続インピーダンス測定結果の解析に使用することができます。
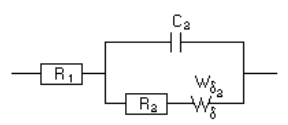
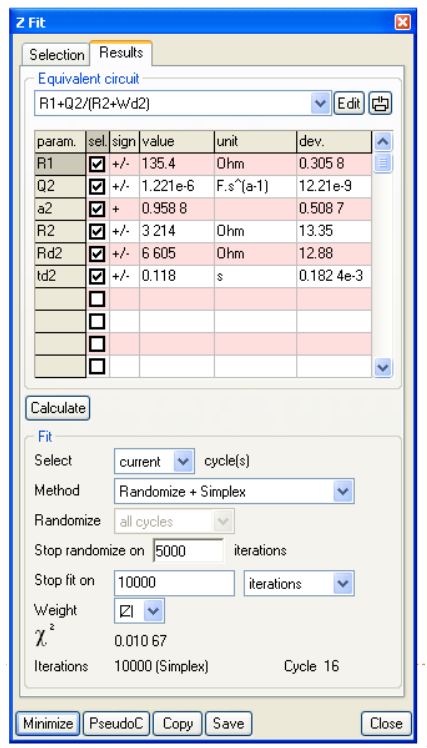
図12 等価回路とZFitウインドウ
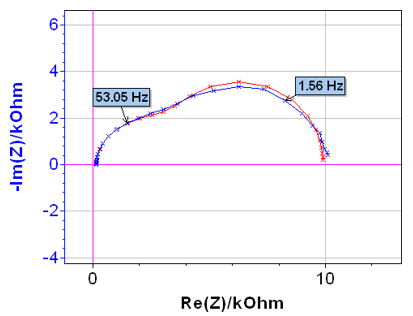
図13 サイクル16のナイキスト図(青色)とフィッティング結果(赤色)
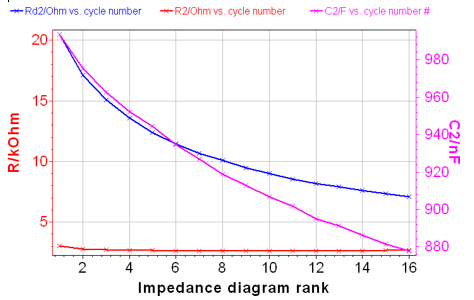
図14 R2、Rd2、およびC2の時間変化
4.結論
SPEIS法は、ユーザが定常曲線または非定常曲線に沿ってEIS測定を行うことのできる測定テクニックです。さらに、EC-Lab®(またはEC-Lab®Express)ソフトウェアに搭載されているZFitを用いることで、連続したインピーダンスプロットを一度に分析することが出来ます。
参考文献
1) Application Note #9 “Linear vs. non-linear systems in impedance measurements”
2) J.-P. Diard, B. Le Gorrec, C. Montella, J. Electroanal. Chem., 432 (1997) 27-39.
3) Application Note #10 “Corrosion current measurement for an iron electrode in an acid solution”
4) Application Note #14 "ZFit and equivalent electrical circuits"
5) M. Chatenet, F. Micoud, I. Roche, E. Chainet, Electrochim. Acta, 51 (2006) 5459.
6) M. B. Molina-Concha, M. Chatenet, J.-P. Diard, in: C. Gabrielli (Ed.) Proceedings of the 20th Forum sur les Impédances électrochimiques, Paris (2007).
7) G. Parrour, Etude du mécanisme d'électrooxydation du borohydrure de sodium, Rapport de Master, Institut Polytechnique de Grenoble, 2008.
電気化学測定装置のお取り扱いページへ
お問い合わせ先
株式会社東陽テクニカ 脱炭素・エネルギー計測部
