電気化学インピーダンス測定におけるドリフト補正
電気化学インピーダンス測定におけるドリフト補正
本内容はBiologic社が発行するApplication note #17を2020年7月時点で翻訳したものです。
今後、原文が改訂され、内容が変更された場合には、改訂後の原文の内容を優先いたします。
導入
電気化学分野でインピーダンス測定を行う場合にはいくつかの適用条件があり、線形性・不変性・因果性の3点になります。実際、サンプルが定常状態に達していない場合、インピーダンス測定の適用条件を満たすことができず、測定結果に影響を及ぼします。
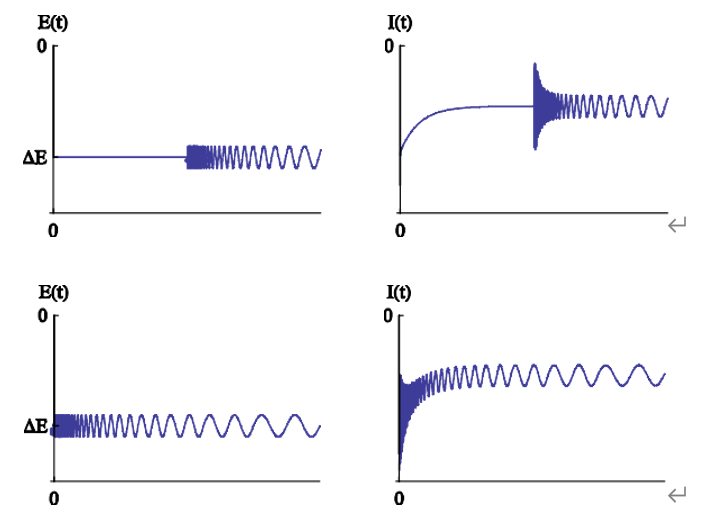
図1 直流電圧ΔEと振幅電圧δEの印加時の電流応答の例
(上:定常状態に達したときに開始した場合、下:定常状態に達する前に開始した場合)
本内容は、定常状態に向かうなかでインピーダンス測定を行う場合のドリフト補正について記載します。入力信号と出力信号のフーリエ変換を使用して、ドリフト補正を行います。最初に電気回路の測定誤差の例を示し、次にドリフト補正なし・ありの場合でリチウムイオン電池の測定結果の比較を示します。
実験
本内容に記されているすべてのインピーダンス測定値は、EC-Lab® Expressソフトウェアのインピーダンス測定テクニック(図2を参照)を使用して取得されたものであり、一般的に振幅電圧はVa = 10 mVです。測定ごとに異なるサイクルが実行されています(測定は連続して実行されています)。
注意:ドリフト補正の機能はEC-Lab®ソフトウェアでも利用できます。
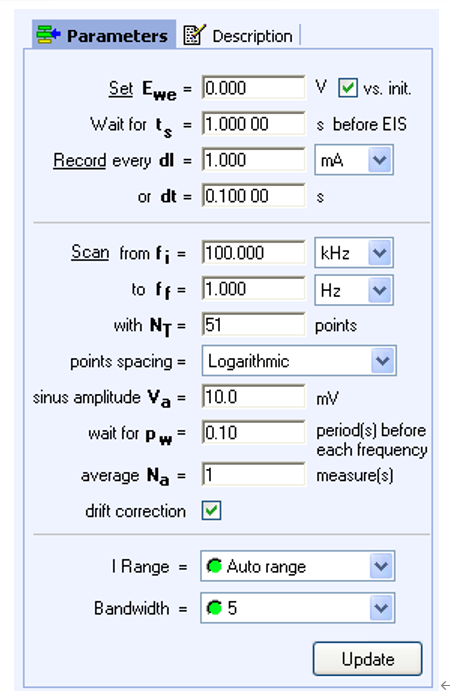
図2 EC-Lab® Expressソフトウェアのドリフト補正ボックスに
チェックを入れたPEISテクニック画面
非定常状態でのインピーダンス測定
テスト電気回路
図3は、3つのコンデンサと2つの抵抗から構成される電気回路を示しています。
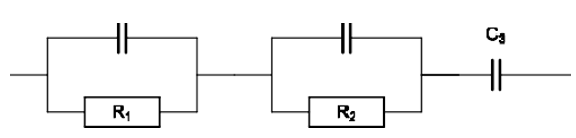
図3 テスト電気回路
この電気回路は、振幅電圧による線形性の適用範囲を示す場合に用いられています[1]が、この回路を例に用いることでドリフト補正の方法を示すことができます。図4は、電気回路の印加電圧に対する応答電流を示しています。約2分後、電流値がゼロに近いことに注目します。つまり、この電気回路のインピーダンス測定をする場合には、測定を開始する前に定常状態になるまで2分間待機する必要があります。
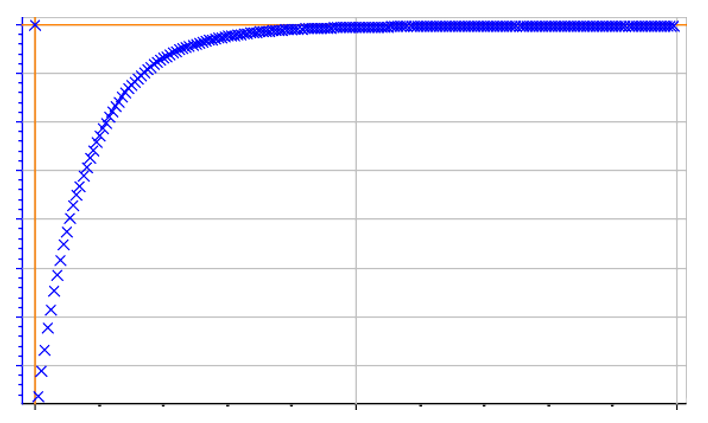
図4 電気回路(図3)の印加電圧に対する応答電流
定常状態を待たずに連続して測定した電気回路(図3)の3つのインピーダンススペクトル(ナイキスト線図)を図5に示します。
2つの半円の頂点周波数(時定数)を図に示しています。2回目と3回目のサイクルは互いに近く、開回路電位で得られたスペクトルと一致しています。測定時間は合計約8分で2回目と3回目のサイクルは定常状態で測定されていますが、1回目のスペクトルには当てはまりません。定常状態に到達するには長い時間がかかる可能性があり、連続測定を行う場合には測定時間がさらに長くなる恐れがあります。
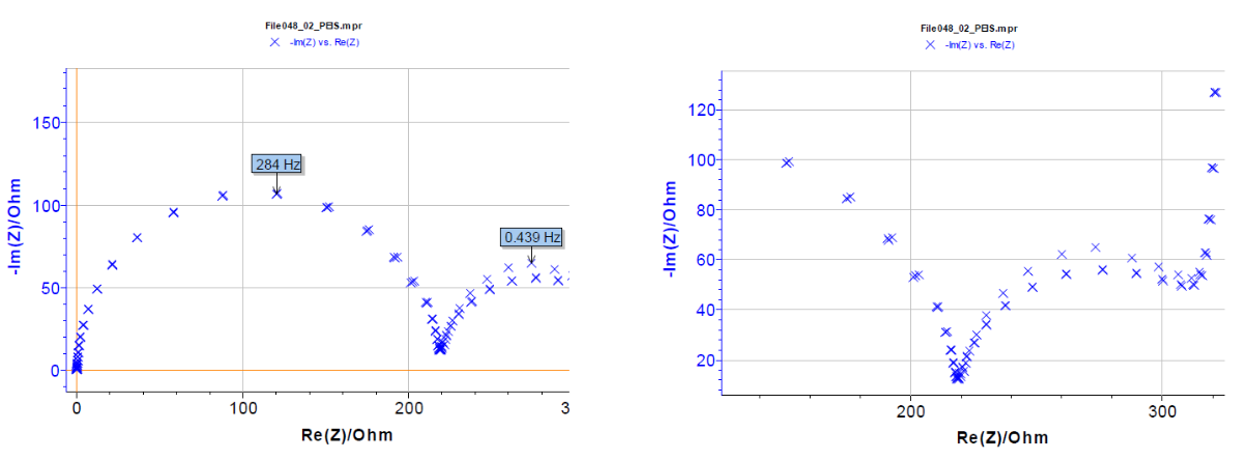
図5 電気回路(図3)の3つのインピーダンススペクトル(ナイキスト線図)
(fmin = 20mHz、fmax = 100kHz(測定点:51ポイント)、Ewe = 50mV、Va = 10mV)
非定常状態でのドリフト補正の原理
ドリフト補正を定義するためには、いくつかの方法があります[2, 3, 4-7]。本内容で記載する方法は、フーリエ変換インピーダンス測定に基づいています。この方法は、離散した電圧と電流のフーリエ変換から算出されます。フーリエスペクトル内のfmの隣接周波数fm-1およびfm+1を利用して、次式を用いることで補正を行います。
![]()
![]()
この補正の原理を図6に示します。ドリフトがない場合、ReI(fm+1)、ReI(fm-1)、ImI(fm+1)およびImI(fm-1)は値がなく、ドリフト補正は行われません。
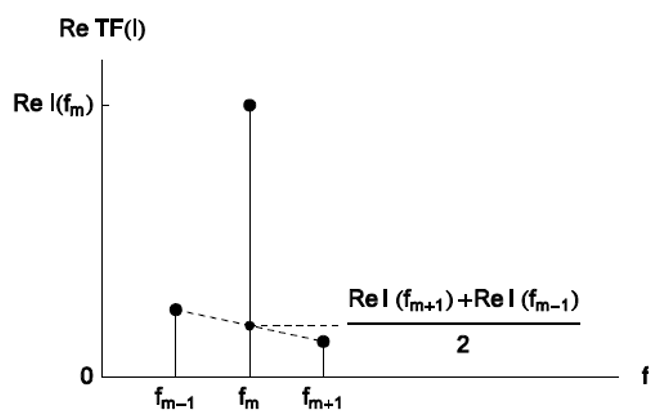
図6 ドリフト補正法の原理(フーリエスペクトルの実部)
図3の電気回路のドリフト補正の例を図7に示します。これらの測定値は、図5と同じ測定条件で測定されました。3つのスペクトルは重なっており、開回路で得られたスペクトルと一致しています。非定常状態でのドリフト補正は、直流電圧が印可されたインピーダンス測定の時間を短縮します。
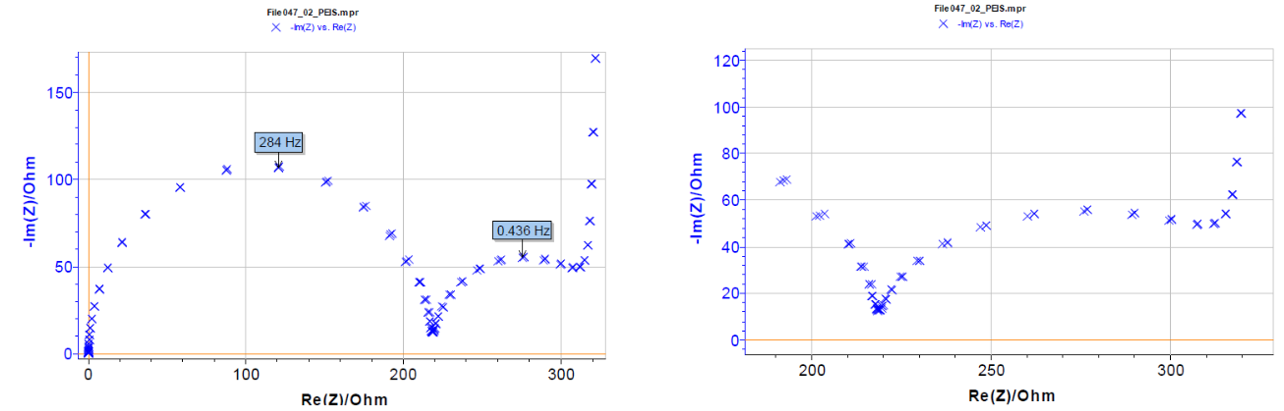
図7 図3のドリフト補正を行った3つのインピーダンススペクトル(ナイキスト線図)
リチウムイオン電池の測定例
このドリフト補正は、1.35Ahのリチウムイオン電池にて適用されました。リチウムイオン電池の特性評価は、規定の電流および電圧による充電/放電および休止(開回路)状態を組み合わせて行います。添加された活物質から電極への拡散係数が低い(~10-12mol/㎠)ため、この緩和時間は非常に長くなる可能性があります。実際、図8はこの電池の印加電圧に対する応答電流と、平衡状態に達する間に必要な時間(~1時間00分)を示しています。
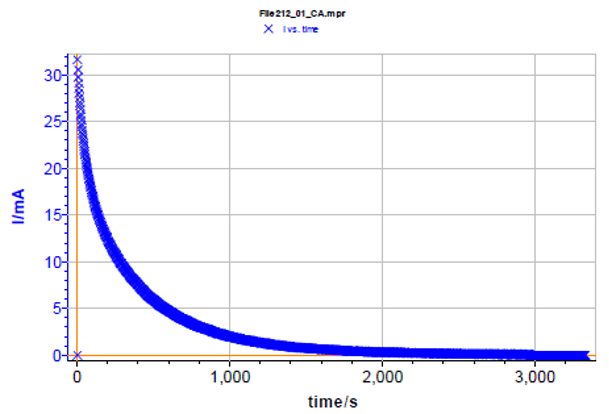
図8 リチウムイオン電池の応答電流(Eoc = 3.09V)
ドリフト補正なし
電圧掃引しながらインピーダンス測定を行ったリチウムイオン電池の2つのナイキスト線図を図9に示します。これらは前述したインピーダンス測定条件で測定し、測定時間は約1時間20分です。これら2つの波形は異なるサイクルとなり、主に低周波数領域で大きな違いがあります。
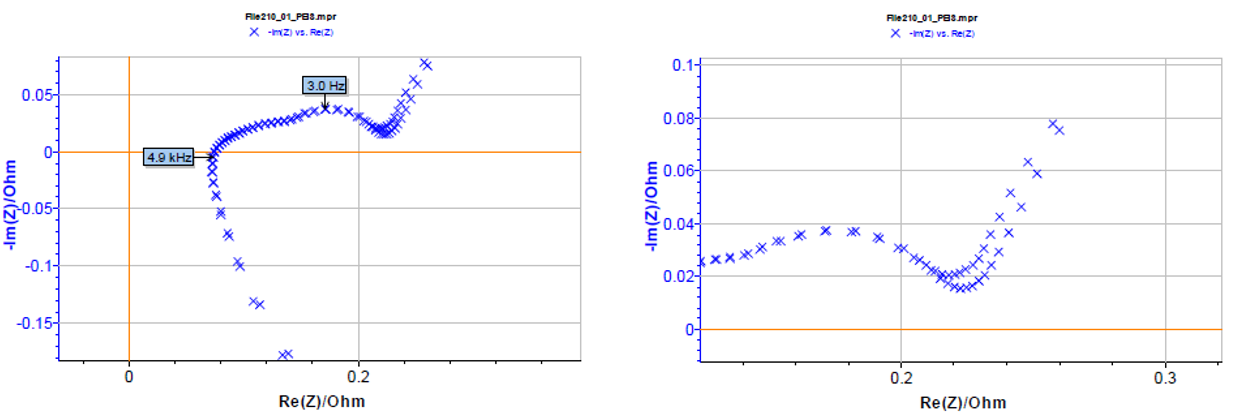
図9 ドリフト補正なしのリチウムイオン電池のナイキスト線図
(fmin = 5mHz、fmax = 10kHz(測定点:51ポイント)、ΔE = 3mV、Eocv = 3.09V)
ドリフト補正あり
ドリフト補正を行ったリチウムイオン電池のナイキスト線図を図10に示します。これら2つのインピーダンススペクトルは、低周波数領域でも非常に近い値を示しています。ドリフト補正により、ユーザは電池のインピーダンス測定時間を短縮できます。
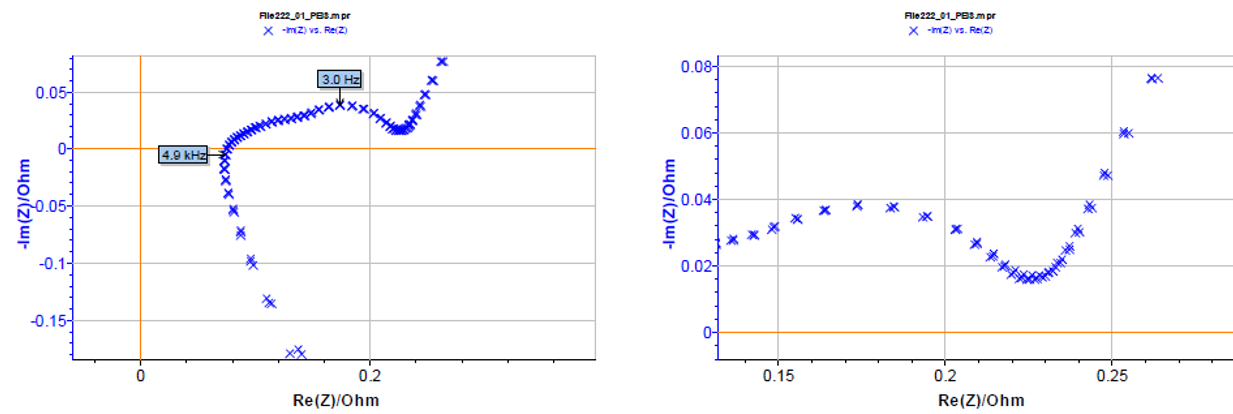
図10 ドリフト補正ありのリチウムイオン電池のナイキスト線図
(設定条件は図9に同じ)
EC-Lab®ソフトの電池評価向け
その他機能紹介(セミナー動画)
結論
本内容で記載されているドリフト補正は、2つの正弦波形を用いることで簡単に行うことができます。この方法は、非常に長い緩和時間を持つ測定系でインピーダンス測定を行う際に適しており、補正に使用されるフーリエスペクトルのポイント数を増やすことで改善できます。例えば、ベースラインを2次(またはそれ以上)の多項式関数でモデル化することもできます。
次のような電気化学測定では、時間安定性がない場合が多くあります。
- 電極で発生する腐食反応
- 充電または放電中の電流制御インピーダンス測定
実際、非定常状態での測定では、定常状態と比較してインピーダンススペクトルにわずかな違いを引き起こす可能性があります。
参考文献
1) Application Note #9 “Linear vs. non linear systems in impedance measurement“
2) A. S. Mc Cormack, J. O. Flower, K. R. Godfrey, IEEE Trans. Instrum. Meas., 43 (1994) 232.
3) R. Pintelon, J. Schoukens, System Identification, IEEE Press, New York, USA (2001).
4) B. Petrescu, Thèse de l’Institut National Polytechnique de Grenoble et de l’Université
”Politehnica” de Bucarest (2002).
5) B. Petrescu, J.-P. Petit, J.-C. Poignet, Brevet français n°02/08897.
6) B. Petrescu, J.-P. Petit, J.-C. Poignet, US patent n°2006/0091892 A1.
7) B. Petrescu, J.-P. Diard, in : C. Gabrielli (Ed.), 20th forum on electrochemical impedance, Paris,
(2007) C219.
電気化学測定装置のお取り扱いページへ
お問い合わせ先
株式会社東陽テクニカ 脱炭素・エネルギー計測部
