シーケンス / 関数top
疲労寿命推定に関するFAQ
Q疲労寿命推定、S-N線図の作成
疲労寿命推定
頻度解析の結果を利用する典型的な例としては疲労寿命推定があります。
ここでは、S-N線図を用いて材料・製品等の疲労寿命を推定する方法について説明します。
S-N線図とは下図のような曲線で、応力(S)と繰り返し回数(N)の関係を表しており、材料・製品自体の特性を示すものです。
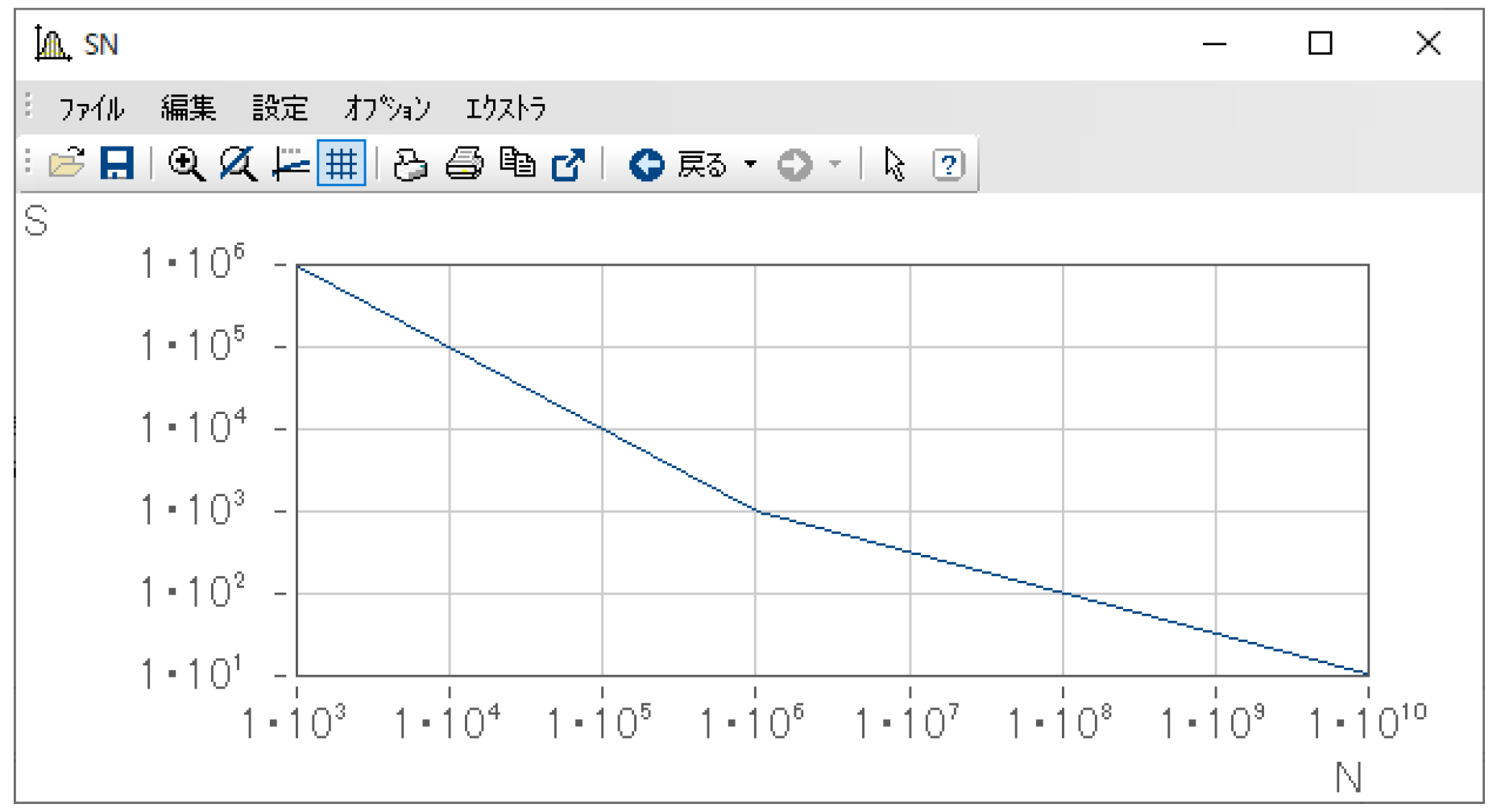
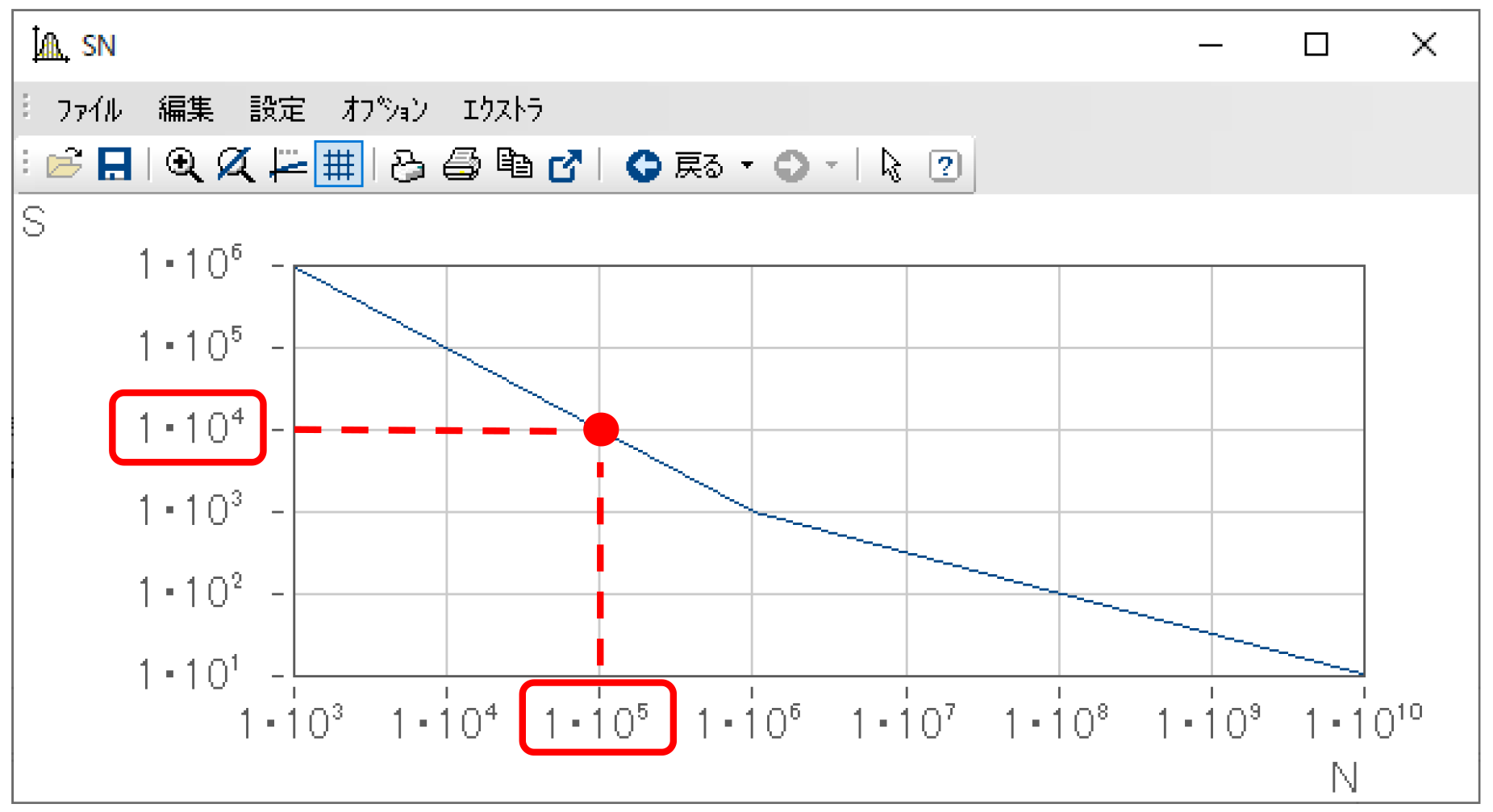
例えば下図に示す1点に着目してみましょう。
これは、このS-N線図が示す対象は、10^4程度の応力(S)を加えられた場合、10^5程度の繰り返し回数で破断・破壊されるということを意味します。
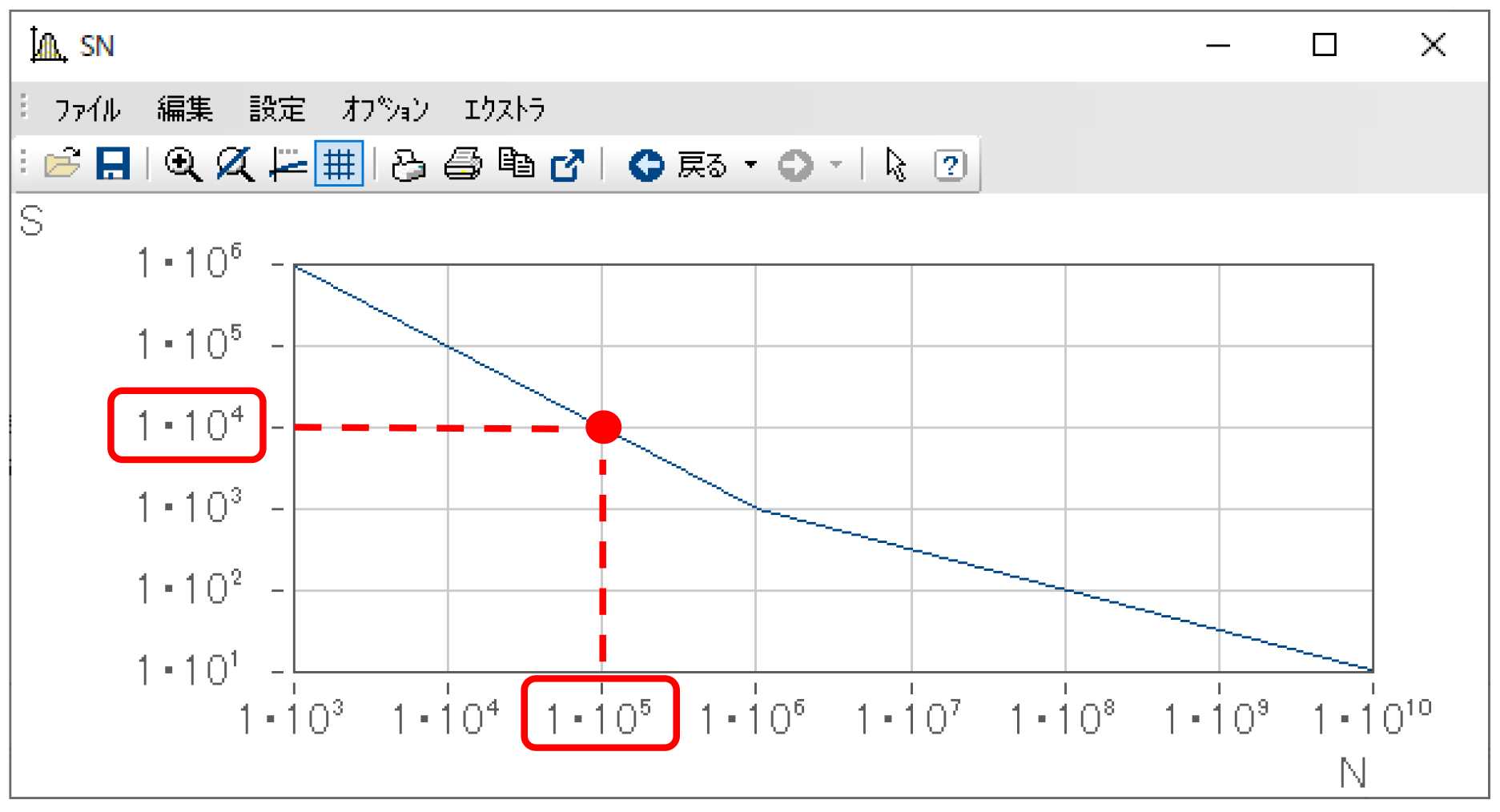
疲労寿命推定では、このS-N線図を元に、まず「ダメージ」を見積もります。
先ほど説明した1点、10^4程度の応力(S)を加えられた場合、10^5程度の繰り返し回数で破断・破壊される、ということは、10^4程度の応力が「1回」加えられた時のダメージは1 / 10^5、と言い換えることができます(=ダメージの累計が1で破断・破壊)。
同じことがすべての応力の値に対して考えられるので、試験データを頻度解析した結果からは、その試験での累計のダメージ、を求めることができます。
そこから、対象の疲労寿命を推定できます。例えば以下のような考え方です。
| 試験データの累計ダメージ | 0.02 |
|---|---|
| 試験データが示す時間(実際の動作環境に換算する) | 10h |
| 推定される疲労寿命 | 10h / 0.02 = 500h |
「試験データが示す時間」は、例えば車両であれば距離[km]で表現してもよいでしょう。その場合は疲労寿命も距離[km]の単位で求められることになります。
次項より、実際にimc FAMOSで疲労寿命推定を行う場合のシーケンス記述について説明していきます。
S-N線図の作成
S-N線図の作成は以下のようにSの配列、Nの配列を作成してそれぞれの値を指定し、それを結合する形で作る方法が簡単です。
作成されたS-N線図のデータはファイルとして保存しておけば、以後の解析に使いまわせます。
; 配列の作成
_S = Ramp(0, 1, 3) ; 最後の3が配列の長さ
_N = Ramp(0, 1, 3)
; S/Nそれぞれの値の設定
_S[1] = 1e6
_S[2] = 1e3
_S[3] = 1e1
_N[1] = 1e3
_N[2] = 1e6
_N[3] = 1e10
; 結合、N(=横軸)が先であることに注意
SN = XYof(_N, _S)
Qダメージ計算:クラスカウント法向け
クラスカウント法の場合、カウント結果は0から始まるインデックスでクラスに分類されています。例としては下図のような状態です。
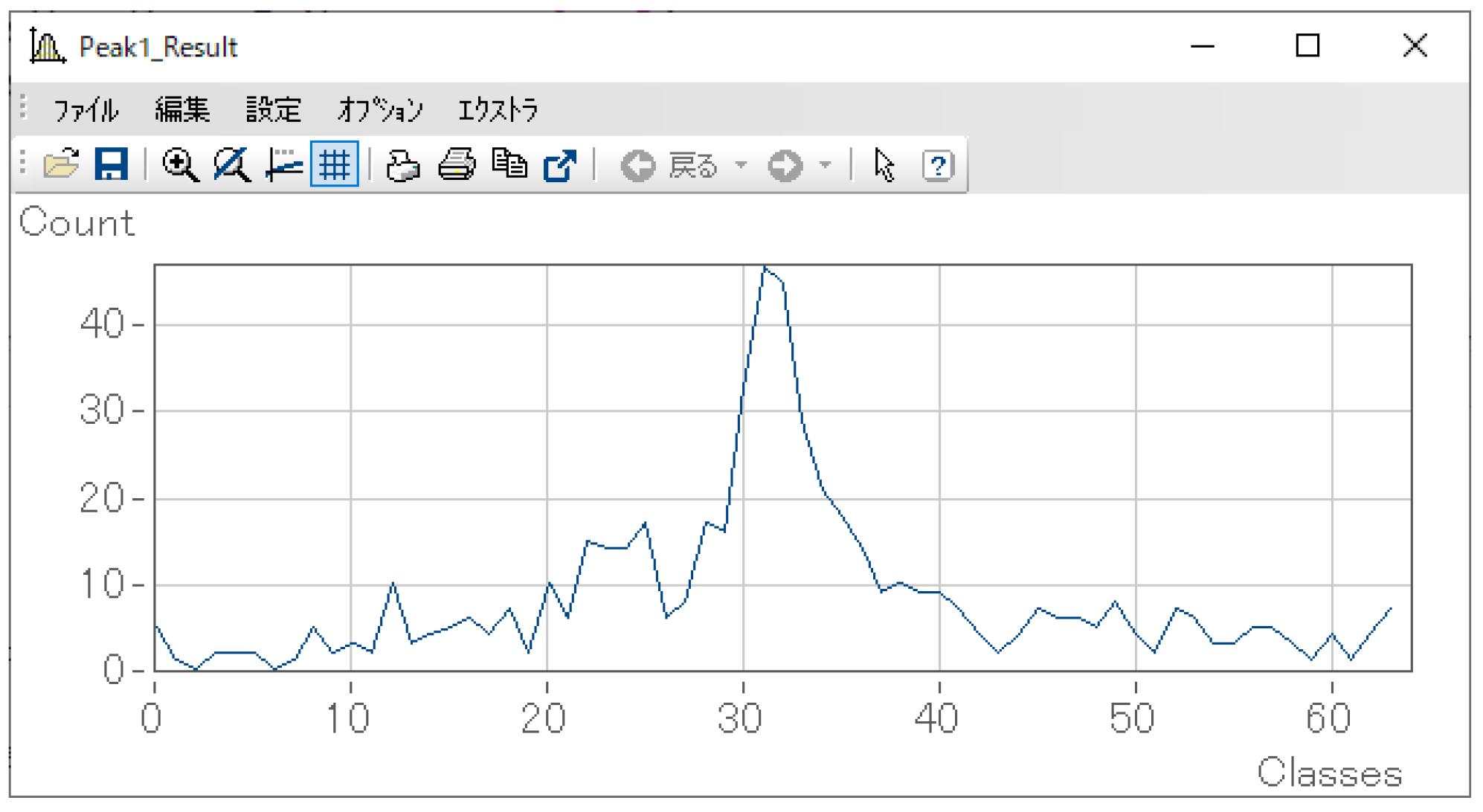
S-N線図では応力Sとして物理単位が使われるため、シーケンスではクラスのインデックスから物理単位に換算して計算を行う必要があります。
ここでは、それぞれ以下の名前を変数として使います。
| SN | S-N線図、応力Sの単位系はクラスカウント法の対象としたデータと同じ |
|---|---|
| Result | クラスカウント法のカウント結果 |
| _MaxValue | カウントしたレンジの上限 (ClsPeak〇関数に使ったパラメータ) |
| _MinValue | カウントしたレンジの下限 (ClsPeak〇関数に使ったパラメータ) |
| _NumberOfBins | 分類されたクラス数 (ClsPeak〇関数に使ったパラメータ) |
| Damage | S-N線図とカウント結果から求められたダメージ |
| TrialTime | 対象データが示す時間、距離など |
| LifeTime | 推定された疲労寿命 |
シーケンスの記述は以下のようになります。
; S-Nを両対数スケール上で検索するために換算
_xlog = Log(SN.X)
_ylog = Log(SN.Y)
; 1クラスのレンジを計算
_range = (_MaxValue - _MinValue) / _NumberOfBins
; すべてのクラスでループ計算
Damage = 0
_i = 1
While _i <= _NumberOfBins
; そのクラスの振幅、応力Sに相当する
_class = Abs(_MinValue + _range * _i)
; 対応する回数NをS-N線図から検索する
_slog = PosiEx(_ylog, Log(_class))
_nlog = Value2(_xlog, _slog, 0)
_N = 10^_nlog
; ダメージに換算する
Damage = Damage + Result[_i] * (1 / _N)
_i = _i + 1
End
; 疲労寿命の推定
TrialTime = 10 ; 対象データ相当の時間/距離などを指定する
LifeTime = TrialTime / Damage
S-N線図が両対数スケールのため、応力Sから回数Nを検索する手順が少々特殊ですが、要点としては「クラスに対応する応力Sを求める」「応力Sに対応する回数Nを求める」「回数Nをダメージに換算して累計を取る」の3点のみです。
Qダメージ計算:レインフロー法向け
レインフロー法の場合、専用の関数が存在しており簡単な記述で疲労寿命推定を行うことができます。
ここでは、それぞれ以下の名前を変数として使います。
| SN | S-N線図、応力Sの単位系はレインフロー法の対象としたデータと同じであり、レンジ(振動の最大値-最小値)でスケールが記述されている必要があります。 |
|---|---|
| ClsHandle | ClsOffRainflowInit1関数で作成された変数(データを与えカウントまで完了していること) |
| Damage | S-N線図とカウント結果から求められたダメージ |
| TrialTime | 対象データが示す時間、距離など |
| LifeTime | 推定された疲労寿命 |
シーケンスの記述は以下のようになります。
; ダメージ計算、後ろ2つのパラメータは任意に指定する
Damage = ClsOffWoehlerSN(ClsHandle, SN, _ClassRelation, _Interpolation)
; 疲労寿命の推定
TrialTime = 10 ; 対象データ相当の時間/距離などを指定する
LifeTime = TrialTime / Damage
ClsOffWoehlerSNのパラメータが示す意味は以下の通りです。
ClsOffWoehlerSN(ClsHandle, SN, _ClassRelation, _Interpolation)
| ClsHandle | ClsOffRainflowInit1関数で作成された変数 |
|---|---|
| SN | S-N線図 |
| _ClassRelation | カウントのクラスは実際には幅があるが、その幅の中でどの程度の応力と見積もるかの設定 0:クラス全体の範囲で等しく分布していると考えます 1:クラスの最大値であると考えます (=最もダメージが大きくなる) 2:クラスの中間点であると考えます |
| _Interpolation | S-N線図の補間の仕方 0:S-N線図は両対数スケールとして補間する 1:S-N線図は応力Sがリニア、回数Nが対数スケールとして補間する |