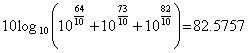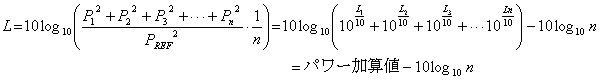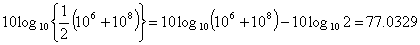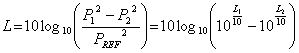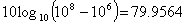シーケンス / 関数top
スペクトラムキット&周波数解析関係に関するFAQ
Qパーシバルの定理について
FAQ ID:p018
理論的に、パワースペクトラムの積分値と時間信号の二乗平均とが等価とならねばなりませんが、うまくあいません。
上記内容はパーシバルの定理といいます。この定理は周波数軸上でのエネルギと時間軸上でのエネルギが保存されるという定理です。
以下にサンプルシーケンスを紹介します。
;------------------------------ ;テストデータ作成 ; 2つの波形を合成しています。 ;------------------------------ datanum=1024 freq1 = 10 ;[Hz] gain1 = 0.5 freq2 = 20 ;[Hz] gain2 = 0.8 data = gain1*cos(ramp(0,pi2/datanum,datanum)*freq1)+ gain2*cos(ramp(0,pi2/datanum,datanum)*freq2) data = XDel(data,1/datanum) ;------------------------------ ;スペクトラムを求めます ; 関数Specは両側スペクトラム ; 関数FFTは片側スペクトラム ; この2つの関係はSpec=2*FFTです ;------------------------------ res=Spec(data) ;------------------------------ ;パワースペクトラムから算出したエネルギ ; FAMOSではFFT結果の振幅をピークで算出するので ; Sqrt(2)で除算しています ; ;Spec関数について納得できなければスペクトラムキット関数を ; 参照してください ;------------------------------ fftres=sum(res.M*res.M)/2 ;------------------------------ ;RMSから算出したエネルギ ;------------------------------ rmsres=RMS(data)*RMS(data) ;------------------------------ ;スペクトラムキット関数からパワースペクトラムを算出したエネルギ ; この結果を利用することにより、Spec関数で除算したSqrt(2)が ; 不要になります ;------------------------------ res2 = PowerSpectrum_1(data, datanum, 0, 0, 1) fftres2=sum(res2
QVibrationFilterのサンプリング周波数
FAQ ID:p015
FAMOSのスペクトラムキットにある"VibrationFilter"を実行させたところ、以下のエラーメッセージが表示されました。

このエラーの意味と対応方法を教えてください。
エラーメッセージは以下の通りです。
VibrationFilter(...): アナログフィルターの係数が有効でないか、サンプリングレートが適合していません。
VibrationFilter関数はISO2631に従い、指定された周波数重みを作成します。この周波数重みはアナログフィルターの係数を指定して計算しますが、この係数が間違っているか、解析したい信号のサンプリング周波数が低いことを意味しています。
アナログフィルターはこの関数が内部で使用していますのでユーザーの設定には関係ありません。恐らく解析したい信号のサンプリング周波数が低いことが予測されます。
各周波数重みに対して周波数バンドは以下のようになっています。
ISO 2631-1, 2nd edition, 1997 に準拠した周波数特性
|
10 |
Wk, Z方向、頭部を除いた横臥姿勢での垂直方向(z) |
|
11 |
Wd, X・Y方向、横臥姿勢での水平方向(X,Y) |
|
12 |
Wf, 乗り物酔い |
|
13 |
Wc, シートバックの測定 |
|
14 |
We, 回転振動の測定 |
|
15 |
Wj, 横臥姿勢での頭部の振動 |
処理したい信号は以下の周波数より高くなければなりません。
|
10 |
>200Hz |
|
11 |
>200Hz |
|
12 |
>1.26Hz |
|
13 |
>200Hz |
|
14 |
>200Hz |
|
15 |
>200Hz |
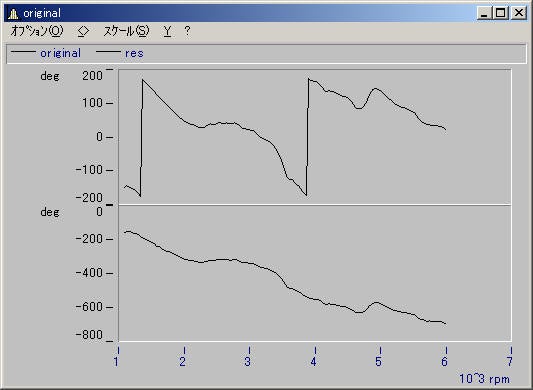
Q位相データを連続で表示するには?
Q周波数データの微分・積分
FAQ ID:p013
周波数データの微分・積分は角速度の乗算・減算より求めます。
条件
OROSデータがDATAという変数で既に読み込まれていると仮定します。
また、例題として変数”DATA”は速度データとして、微分・積分の例を示します。
サンプル・シーケンス
以下のシーケンスを作成してください。
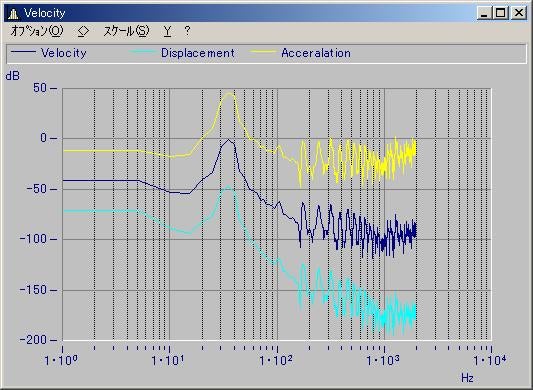
;------------------------------------------- ;DataはOROSで測定した周波数解析結果です。 ;OROS用のインポートフィルターを使用した場合 ;データはdBで出力されますのでリニアに変換します ;------------------------------------------- Velocity = 10^(Data/20)
;------------------------------------------- ;X軸(周波数データ)をデータから作成します ;------------------------------------------- Freq = Ramp( XOff?(Velocity), XDel?(Velocity), Leng?(Velocity))
;------------------------------------------- ;積分(変位) ;積分して、オリジナル比較できるようにdBに変換します。 ;------------------------------------------- Displacement = dB( Velocity / PI2 / Freq )
;------------------------------------------- ;微分(加速度) ;微分して、オリジナル比較できるようにdBに変換します。 ;------------------------------------------- Acceralation = dB( Velocity * PI2 * Freq )
結果
注意:
詳細は信号処理関連の文献を参照してください。
Q校正信号を使い、この値を74dBとしたい
FAQ ID:p010
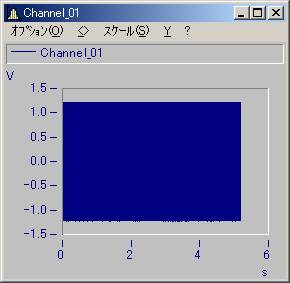
騒音計から測定した校正信号をパソコン上でdB変換するとMAXが0dBになってしまいます。74dBにするにはどうすればよいですか?
74dBの校正信号を添付しますので、FFT画面でピーク値を74dBに合わせてもらえないでしょうか。
;測定した時系列信号は以下のように変換されdB表示されます。
; dB = 20 * Log( 測定値 / 参照値)
;従って、今回この式を使って、
; dB = 74
;に相当する参照値を測定値から求めればよいことがわかります。
;-----------------------------------------------------------
;それでは実際に値を求めてみましょう
;-----------------------------------------------------------
;最初にFFTのピーク値を求めます。
_res_Y = Max( Cmp1( Spec( Channel_01 )))
;一般に音の評価では実効値で評価します。
_res_Y =_res_Y / Sqrt(2)
;この信号より、参照値を求めます。
_res_REF = _res_Y / (10 ^( 74 / 20))
;-----------------------------------------------------------
;以上で準備は完了です。
;-----------------------------------------------------------
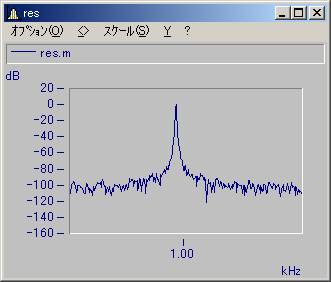
;求めた参照値を使ってFFT演算して結果を表示してみましょう。
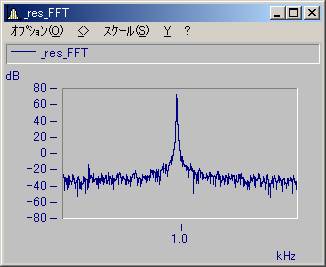
_res_FFT = Spec( Channel_01/_res_REF)
_res_FFT = db(_res_FFT.M / Sqrt(2))
Show _res_FFT
;ピーク値は74dBになっています。
Q1/3オクターブから1/1オクターブを算出
Qパワー加算
FAQ ID:p012
音圧をP1,P2,・・・,Pnとして、これに対応した参照レベルを考慮したdBレベル値をL1,L2,・・・,Lnとします。
これらの関係は以下のようになっています。
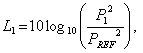
ここで、PREFは音圧では2E-5Paなどの参照値です。
これらの加算値は以下のように計算できます。
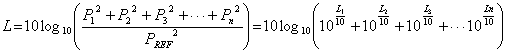
【Example】
60dBと80dBの加算値は以下のようになります。
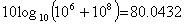
【Example】
リニア値では以下のようになります。
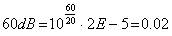
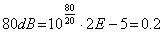
これらのリニア値に対して二乗して加算します。
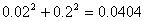
このdB値を算出します。
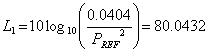
【Example】
オーバーオール値の計算は以下のようになります。
20 * Log( Sqrt( Sum( idB( DATA)^2) / 1.5))
ここで、
DATAはdBの値です。
1.5は等価ノイズバンド幅です。
等価ノイズバンド幅:
1.5 = ハニング
Qパワー平均
Qパワー減算
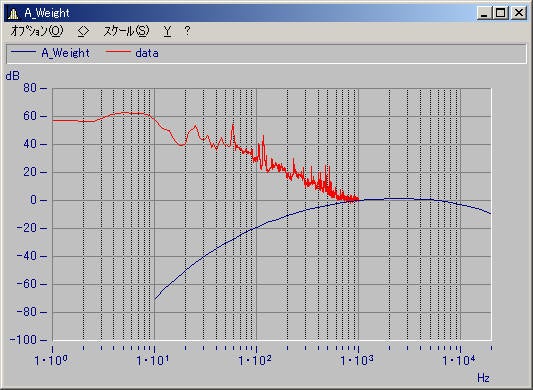
QFFT結果に後からA特性を適用する
Qウィンドウ関数について
FAQ ID:p003
- Rectangular
- Hanning
- Hamming
- Blackmann
- Blackman-Haris
- Flat-Top
各ウィンドウは様々な特性を持っています。ウィンドウを選択する際には信号の周波数特性を予め把握しておく必要があります。信号が対象とする周波数から離れた周波数に強いノイズを含む場合、高いサイドローブの傾きが必要になります。
信号が様々な信号から構成され互いに接近している場合、スペクトラム分解能が重要になります。この場合、狭いメインローブを選択するとよいです。信号の振幅が重要な場合には広いメインローブを選択してください。信号が広い周波数範囲に存在する場合にはRectangularを使用してください。一般的にHanningは95%程度のアプリケーションに対応します。
Flat-Topは良い振幅特性を表します。しかし、メインローブが広いので分解能・漏れの特性が良くありません。
インパクトなどの過渡的な信号を解析する場合には、ウィンドウを使用しないほうが良いです。ウィンドウを使うとサンプルの最初で重要な情報が欠落してしまいます。代わりにForce、Exponentialを使用してください。
アプリケーション
- 正弦波・正弦波の集合 Hanning
- 正弦波(振幅特性を重視) Hamming
- 狭帯域ランダム信号 Hanning
- 広帯域ランダム信号 Rectangular
- 近接した正弦波 Rectangular・Hamming
- 加振信号(ハンマー加振) Force
- 応答信号 Exponential
- 未知の信号 Hanning
ウィンドウ関数について
A0-A1*Cos(2*PI*t/T)+ A2*Cos(4*PI*t/T)-A3*Cos(6*PI*t/T)+ A4*Cos(8*PI*t/T)
但し、 T:ウィンドウの時間幅
A0~A4:係数
ノイズバンド幅係数
NBFW=A0^2+0.5*(A1^2+ A2^2+ A3^2+ A4^2)
等価ノイズバンド幅
ENBW=NBFW/T
方形波
|
A0 |
A1 |
A2 |
A3 |
A4 |
|
1 |
0 |
0 |
0 |
0 |
ENBW=1
ハニング
0.5 * [1-cos(2*pi*i/(N-1))]
|
A0 |
A1 |
A2 |
A3 |
A4 |
|
1 |
1 |
0 |
0 |
0 |
ENBW=1.5
ハミング
0.54-0.46*cos(2*pi*i/(N-1))
|
A0 |
A1 |
A2 |
A3 |
A4 |
|
1 |
0.85 |
0 |
0 |
0 |
ENBW=1.36
カイザーベッセル
|
A0 |
A1 |
A2 |
A3 |
A4 |
|
1 |
1.238 |
0.244 |
0.002 |
0 |
ENBW=1.8
フラットトップ
|
A0 |
A1 |
A2 |
A3 |
A4 |
|
1 |
1.933 |
1.286 |
0.388 |
0.033 |
ENBW=3.77
Triangular
1.0 - |(i-0.5*(N-1))/(0.5*(N-1))|
Welch
1-((i-0.5*(N-1))/(0.5*(N+1)))^2
ブラックマン
(0.42/0.42)-(0.5/0.42)*cos(2*pi*i/(N-1))+(0.08/0.42)*cos(4*pi*i/(N-1))
ブラックマン-ハリス
(0.35875/0.35875)-(0.48829/0.35875)*cos(pi*i/(N-1))+(0.14128/0.35875)*cos(2*pi*i/(N-1))-(0.01168/0.35875) *cos(3*pi*i/(N-1))
Parzen
1.0 - |(i-0.5*(N-1))/(0.5*(N+1))|
;-------------------------------------------------------------- wintype=3 fftoption wintype 0 window = ifft( fft( Leng( 0, 1024)+1)) temp=fft(window) enbw=max( temp.m)
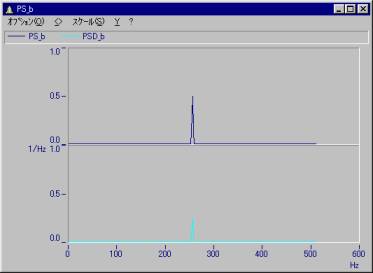
Qパワースペクトル密度関数(PSD)の計算
FAQ ID:p008
計算結果を比較するために1ブロックを256点として、1番目の区間と2番目の区間、1&2をまとめた区間を考えます。
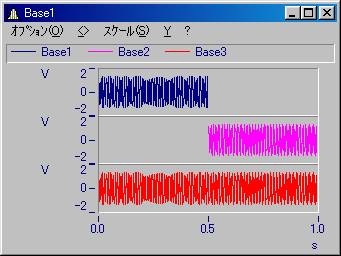
振幅スペクトラムの結果
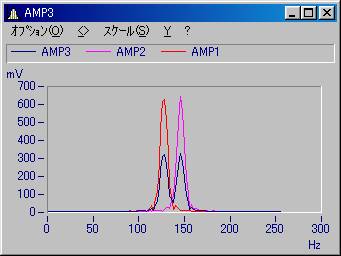
1ブロック 0.63282
2ブロック 0.010443
トータル 0.321632
パワースペクトラム密度関数の結果
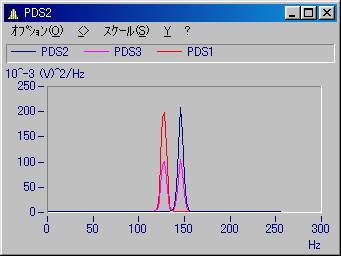
1ブロック 0.200231
2ブロック 0.000054502
トータル 0.100143
振幅スペクトラムの平均された値について
平均化されて算出された値は以下のように算出されます。
平均値 = (1ブロック+2ブロック) / 2
【計算例】
0.321632 = ( 0.63282 + 0.010443 )/2
パワースペクトラム密度関数の平均化された値について
パワースペクトル密度の算出は以下のようになります。
1ブロックのPSD = 1ブロックの振幅スペクトラム^2/周波数分解能(2Hz)
【計算例】
0.0200231 = ( 0.63282^2 )/2
平均化されて算出された値は以下のように算出されます。
平均値 = (1ブロック^2 + 2ブロック^2) / 2 /周波数分解能(2Hz)
【計算例】
0.100143 = ( 0.63282^2 + 0.010443^2 )/2
FFTアナライザーで計算される値との相違
FFTアナライザーなどでは以下のように算出されます。
平均値 = 平均化された振幅スペクトラム^2 /周波数分解能(2Hz)
【計算例】
0.0517236 = ( 0.0321632^2 )/2
また、等価ノイズバンド幅を考慮し
PSD = 平均化された振幅スペクトラム^2 /周波数分解能(2Hz) /等価ノイズバンド幅
等価ノイズバンド幅
Ver6.0までのFAMOS関数は等価ノイズバンド幅を考慮していません。
パワースペクトル密度関数を算出後に各ウィンドウに対応した等価ノイズバンド幅で除算してください。
Ver6.1以降のPowerDS*(), CrossPowerDS*()関数は等価ノイズバンド幅を考慮しているため除算は不要です。
サンプルシーケンス
;************************************************* ;PSD計算について ; データ長が256×2のデータを例にします。 ;************************************************* ;1ブロック目のデータ Base1 = CutIndex( ch__1, 1, 256) PDS1 = PowerDS_1( Base1, 256, 2, 0, 1) AMP1 = AmpSpectrumRMS_1( Base1, 256, 2, 0, 1) ;2ブロック目のデータ Base2 = CutIndex( ch__1, 1+256, 256+256) PDS2 = PowerDS_1( Base2, 256, 2, 0, 1) AMP2 = AmpSpectrumRMS_1( Base2, 256, 2, 0, 1) ;1&2ブロックのデータ Base3 = CutIndex( ch__1, 1, 256+256) PDS3 = PowerDS_1( Base3, 256, 2, 0, 1) AMP3 = AmpSpectrumRMS_1( Base3, 256, 2, 0, 1) ;----------------------------------------- ;1ブロックのピークに相当する各関数の振幅値について考察します。 ;周波数データの分解能は2Hzです。 ;----------------------------------------- A1 = Max(AMP1) Freq = Pos( AMP1, A1) A2 = Value( AMP2, Freq) A3 = Value( AMP3, Freq) ;平均化された値は次式と等価になります CompareA3 = (A1+A2)/2 P1 = Value( PDS1, Freq) P2 = Value( PDS2, Freq) P3 = Value( PDS3, Freq) ;パワースペクトル密度は次式で算出されます。 CompareP1 = A1^2/xDel?(AMP1) ;平均化されたパワースペクトル密度は次式で算出されます。 CompareP3 = (A1^2+A2^2)/2/xDel?(AMP1) ;FFTアナライザーなどで計算される値は次式となります。 CompareFFT = Sqrt(A3^2/xDel?(AMP3)/ENBW)
Q定幅トラッキング分析
FAQ ID:p007
回転数に回転パルスを入力した場合のトラッキング分析のサンプルシーケンスを示します。
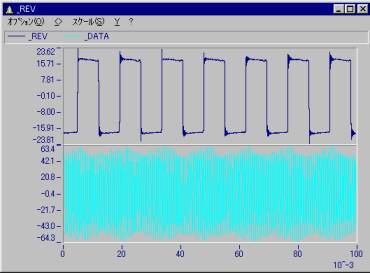
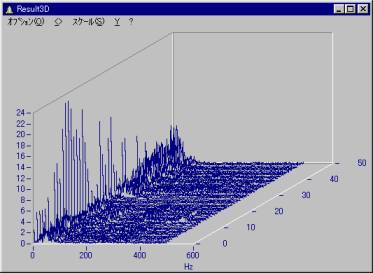
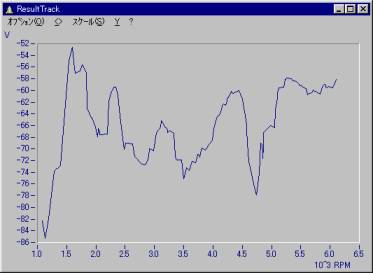
_REV = REV
_DATA = acc
;------------------------------
;エンジンパルスを検索します。
;------------------------------
_res = SearchLevel( _REV, 2, 0, 0, 2, 1, 0, 1)
;回転パルスを検出できない場合、シーケンス終了
_num = Leng?(_res.X)
If _num=0
_Ret = BoxMessage("警告", "回転パルスを検出できませんでした", "!1")
del _*
ExitSequence
End
;------------------------------
;回転数を計算します。
;------------------------------
_res1 = CutIndex( _res.X, 1, _num-1)
_res2 = CutIndex( _res.X, 2, _num)
_DiffTime = _Res2-_Res1
_res.Y =
_DiffTime
_res[_num].Y = _res[_num-1].Y
;------------------------------
;定幅FFT解析
;------------------------------
_WindowWidth = 256
_Result3D =
AmpSpectrumRMS( _DATA, _WindowWidth, 2, 0, 1, 0)
;------------------------------
;
トラッキングデータの取得
;------------------------------
_BlockTime = _WindowWidth * XDel?( _DATA)
_Order = BoxValue?("取得したい次数を入力してください",1,0)
_SegNum = Leng?( _Result3D)/SegLen?(_Result3D)
_ResultTrack = XYof( Leng( 0, _SegNum), Leng( 0, _SegNum))
_i=1
While _i<=_SegNum
_ResultTrack.X = ReplIndex( _ResultTrack.X, 60*1/Value( res,
_BlockTime*(_i-1)), _i)
_Value = Value( _Result3D[_i], _ResultTrack[_i].X/60*_Order)
_ResultTrack.Y = ReplIndex( _ResultTrack.Y, _Value, _i)
_i=_i+1
End
XUnit _ResultTrack rpm
;------------------------------
;結果の保存
;------------------------------
ResultTrack=_ResultTrack ;次数データ(回転数 vs. 次数データ)
Result3D = _Result3D ;3D FFT結果
show ResultTrack
show Result3D
_Ret = BoxMessage("注意", "Result3Dはウォーターフォール表示に
してください","!1")
del _*
QFFT解析結果を1/3オクターブで表示
FAQ ID:p006
;*********************************************************
;FFT解析結果を1/3オクターブバンドで表示させるサンプル
; FFTした結果は周波数間隔がリニアです。
; 1/3オクターブ表示は対数軸なので、変換が必要になります。
; (高周波では1/3オクターブの1つのバンドに対して
; 複数のFFTした結果が含まれることになります。)
;
;FFT解析結果を変数"_DATA"に予め格納してください
;*********************************************************
;----------------------------
;データ処理する周波数
_StartFreq = 1
_StopFreq = 250
;----------------------------
;----------------------------------------------
;1/3オクターブデータの作成
;このサンプルでは0.1Hzから8000Hzまでのデータを生成しています。
;
; _Startで開始オクターブインデックスを指定します。
; 例: -1=0.1Hz: 0=1Hz: 1=10Hz
;_Octaveでオクターブバンドを指定します。
; 例:3を指定した場合、1~1000Hz
;----------------------------------------------
_Start = -1 ;開始オクターブインデックス
_Octave = 5 ;オクターブバンド
_OctData = GrNew()
;[上側周波数]
_OctData:High = Leng( 0, 10*_Octave)
_OctData:High = XOff( _OctData:High, _Start*10)
;[下側周波数]
_OctData:Low = Leng( 0, 10*_Octave)
_OctData:Low = XOff( _OctData:Low, _Start*10)
;[中心周波数]
_OctData:Center = Leng( 0, 10*_Octave)
_OctData:Center = XOff( _OctData:Center, _Start*10)
_i=1
While _i<=_Octave
;[上側周波数]
_OctData:High[10*(_i-1)+1] =1.12*10^(_Start)
_OctData:High[10*(_i-1)+2] =1.40*10^(_Start)
_OctData:High[10*(_i-1)+3] =1.80*10^(_Start)
_OctData:High[10*(_i-1)+4] =2.24*10^(_Start)
_OctData:High[10*(_i-1)+5] =2.80*10^(_Start)
_OctData:High[10*(_i-1)+6] =3.55*10^(_Start)
_OctData:High[10*(_i-1)+7] =4.50*10^(_Start)
_OctData:High[10*(_i-1)+8] =5.60*10^(_Start)
_OctData:High[10*(_i-1)+9] =7.10*10^(_Start)
_OctData:High[10*(_i-1)+10] =9.00*10^(_Start)
;[下側周波数]
_OctData:Low[10*(_i-1)+1] =0.90*10^(_Start)
_OctData:Low[10*(_i-1)+2] =1.12*10^(_Start)
_OctData:Low[10*(_i-1)+3] =1.40*10^(_Start)
_OctData:Low[10*(_i-1)+4] =1.80*10^(_Start)
_OctData:Low[10*(_i-1)+5] =2.24*10^(_Start)
_OctData:Low[10*(_i-1)+6] =2.80*10^(_Start)
_OctData:Low[10*(_i-1)+7] =3.55*10^(_Start)
_OctData:Low[10*(_i-1)+8] =4.50*10^(_Start)
_OctData:Low[10*(_i-1)+9] =5.60*10^(_Start)
_OctData:Low[10*(_i-1)+10] =7.10*10^(_Start)
;[中心周波数]
_OctData:Center[10*(_i-1)+1] =1.00*10^(_Start)
_OctData:Center[10*(_i-1)+2] =1.25*10^(_Start)
_OctData:Center[10*(_i-1)+3] =1.60*10^(_Start)
_OctData:Center[10*(_i-1)+4] =2.00*10^(_Start)
_OctData:Center[10*(_i-1)+5] =2.50*10^(_Start)
_OctData:Center[10*(_i-1)+6] =3.15*10^(_Start)
_OctData:Center[10*(_i-1)+7] =4.00*10^(_Start)
_OctData:Center[10*(_i-1)+8] =5.00*10^(_Start)
_OctData:Center[10*(_i-1)+9] =6.30*10^(_Start)
_OctData:Center[10*(_i-1)+10] =8.00*10^(_Start)
_Start = _Start+1
_i=_i+1
End
;データ処理する周波数を含むようにインデックスを求めます。
_StartIndex = Floor( Pos( _OctData:Low, _StartFreq))
_StopIndex = Floor( Pos( _OctData:High,
_StopFreq)-0.001)+1
_OctNum = _StopIndex-_StartIndex+1
_OctRes = Leng( 0, _OctNum)
_i=1
While _i<=_OctNum
;FFTデータをオクターブバンド毎に切り出し、その合計値を求めます。
_OctIndex = _StartIndex +(_i -1)
_OctLowFreq = Value(_OctData:Low, _OctIndex)
_OctHighFreq = Value(_OctData:High, _OctIndex)
_OctCutData = Cut( _DATA, _OctLowFreq, _OctHighFreq)
_OctRes[_i] = RMS( _OctCutData)
_i=_i+1
End
;-------------------------------
;他の波形と重ね書きできるようにXY波形にします。
_OctXAxis = Cut( _OctData:Center, _StartIndex, _StopIndex)
OctResult = XYof( _OctXAxis, _OctRes)
Delete _*
Qウォーターフォールデータからトラッキングデータを抽出する方法
FAQ ID:p005
以下のようなウォーターフォールデータと回転数データを対象にします。
ウォーターフォールデータは、以下のようになっています。
X軸:周波数
Y軸:データレベル(縦軸方法)
Z軸:セグメント番号(奥行き方向)
また、回転数データは、以下のようになっています。
X軸:セグメント番号
Y軸:回転数データ
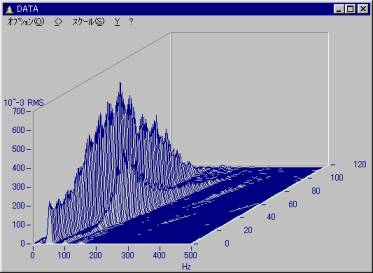
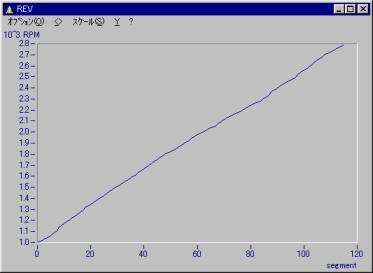
従って、ウォーターフォールのZ軸に回転数のデータを当てはめると通常のウォーターフォール表示になります。
(FAMOSでは、Z軸は等間隔にしか対応していないので、2つのデータに分けています。)
トラッキング解析は、各セグメント(ある回転数の周波数)データに対して、その回転数に対応した周波数のデータを取り出すことです。
ウォーターフォールを上から見ると以下のようになり、緑色で表示されている部分が次数成分に対応します。
回転数と周波数の関係は以下のようになります。

上式より、例えば6000[rpm]のときの2次成分は、200[Hz]となります。
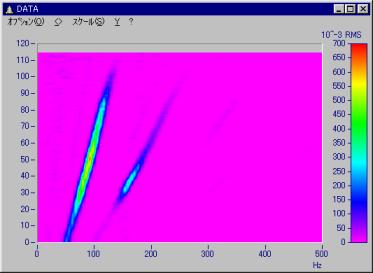
以下にウォーターフォールからトラッキングデータを取得するサンプルシーケンスを示します。
;*************************************************************** ;Order.seq ; 振動波形を次数分析します。 ; ;FAMOSの組込み関数は、青字で表示されます。 ;オンラインヘルプを表示させるためには、カーソルを ;組込み関数の上に持っていき、"Ctrl+F1"キーを押してください。 ;FAMOSメインウィンドウの"Output"ボックスにヘルプが表示されます。 ;*************************************************************** ;------------------------------------ ;次数を設定します。 ;------------------------------------ OR_Order2 = 2 ;次数 OR_Order4 = 4 ;次数 OR_Order_delta = 5 ;[rpm] ;---------------------------------- ;結果を格納する配列を作成します。 ;---------------------------------- OR_Point = Leng?( REV) Result2 = Leng( 0, OR_Point) Result4 = Leng( 0, OR_Point) ResOrderOA = Leng( 0, OR_Point) OR_i = 1 While OR_i<=OR_Point ;2次成分を取り出します。 OR_Temp = Cut( DATA[OR_i], (Rev[OR_i]-OR_Order_delta)/ 60*OR_Order2, (Rev[OR_i]-OR_Order_delta)/60*OR_Order2) Result2 = ReplIndex( Result, RMS( OR_Temp), OR_i) ;4次成分を取り出します。 OR_Temp = Cut( DATA[OR_i], (Rev[OR_i]-OR_Order_delta)/ 60*OR_Order4, (Rev[OR_i]-OR_Order_delta)/60*OR_Order4) Result4 = ReplIndex( Result, RMS( OR_Temp), OR_i) ;OverAllを計算します OR_Temp = Sqrt( SUM( Result[OR_i]^2)) ResOrderOA = ReplIndex ( ResOrderOA, OR_Temp, OR_i) OR_i = OR_i+1 End Result=XYOf( REV, Result) SHow Result del OR_*
Qスペクトラムキットを使用しない場合のFFT演算シーケンス
FAQ ID:p004
;-----------------
;FFTの設定
;-----------------
FFTOption 2 1 ;Window( 0:Rectangular /1:Hamming /2:Hanning /3:Blackman /4:Black
man/Harris /5:Flat-Top )
;Mode( 0:データ低減 /1:データ挿入 )
NumData = 1024 ;データ数
Overrap = 50 ;オーバーラップする率 [%]
RapData = Floor(NumData*(1-Overrap/100) )
;オーバーラップしない部分のデータ数
Delete Overrap
;-----------------
;アベレージ回数の計算
;-----------------
tempNum = Leng?( Data)
temp=1
NumAve=0
While temp<=tempNum-NumData+1
temp=temp+RapData
NumAve=NumAve+1
End
if NumAve=0
NumAve=NumAve+1
End
Delete tempNum
Delete temp
;-----------------
Result = Leng( 0, NumData) ;結果を格納する変数
Delta_F = 1/XDel?( Data)/NumData
Result = XDel( Result, Delta_F)
F1_Count = 1 ;FFT計算回数
F1_Start = 1 ;FFT開始ポイント
While F1_Count <= NumAve
F1_DataCut = CutIndex( Data, F1_Start, F1_Start+NumData-1 )
F1_FFT = Spec( F1_DataCut )
Delete F1_DataCut
Result = Result+F1_FFT.m
F1_Count = F1_Count + 1
F1_Start = F1_Start + RapData
End
Result = Result/(F1_Count-1)
;-----------------
;検証
; スペクトラムキットと比較
;-----------------
Res_Spec = AmpSpectrumPeak_1( Data, 1024, 2, 50, 1)
Delete F1_*
Delete NumData
Delete NumAve
Delete RapData
Delete Delete Delta_F
Q各スペクトラムの計算の違いについて
FAQ ID:p002
スペクトラムキットに組み込まれている
AmpSpectrumRMS
AmpSpectrumPeak
PowerSpectrum
PowerDS
について説明します。
AmpSpectrumRMSとAmpSpectrumPeakの違い
AmpSpectrumPeakは、その振幅を返します。
AmpSpectrumRMSは、その振幅の実効値を返します。
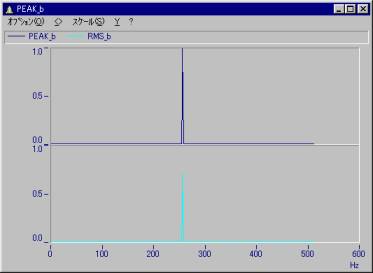
例えば振幅1の正弦波を入力した場合、AmpSpectrumPeakは、その振幅を返します。(=1)
AmpSpectrumRMSは、その振幅の実効値を返します。(=0.707)
PowerSpectrumとAmpSpectrumRMSの違い
AmpSpectrumRMSを2乗したものがPowerSpectrumとなります。
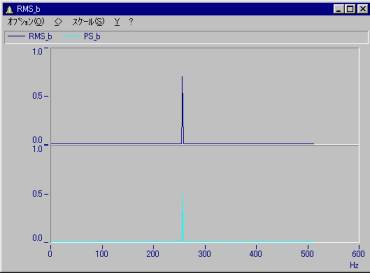
PowerSpectrumとPowerDSの違い
PowerSpectrumを周波数分解能で割った値がPowerDSとなります。
今回の例では周波数分解能を2Hzに設定しています。従って、パワースペクトラムの値を1/2倍したものがパワースペクトラム密度になります。
Q平均化のパラメータについて教えてください。
FAQ ID:p001
引数は以下のように定義されています。
AveragingType
0 平均化なし
1 線形数値平均(平均化されるスペクトルの量はパラメータ'Reduction'によります)
例えば、Reduction=10と指定した場合、1~10th,11~20th...の平均を表示します。
2 ピークホールド(最大)
Reductionの設定に拘わらず、全てのスペクトラムのピーク値をホールドします。
3 低減化されたスペクトルのピークホールド(最大)
Reductionで設定された回数内でのスペクトラムのピーク値を求めます。
4 ピークホールド(最小)
5 低減化されたスペクトルのピークホールド(最小)
スペクトラムキットで周波数計算を行う場合、下図のようにオーバーラップさせながら指定されたウィンドウ長毎に計算します。
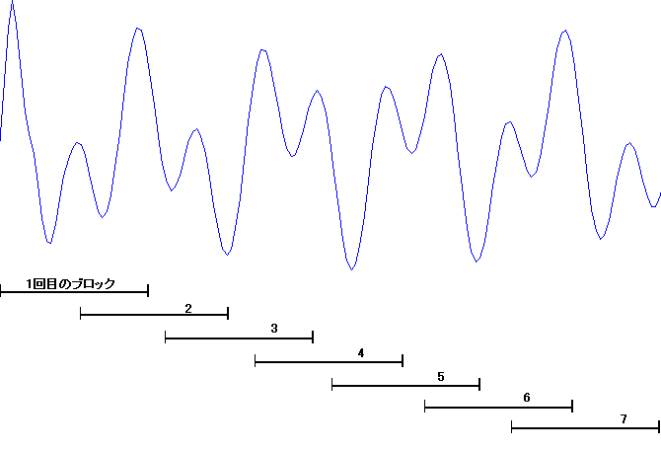
このとき、引数AverageTypeのパラメータを指定することにより、さまざまな結果を取得することができます。
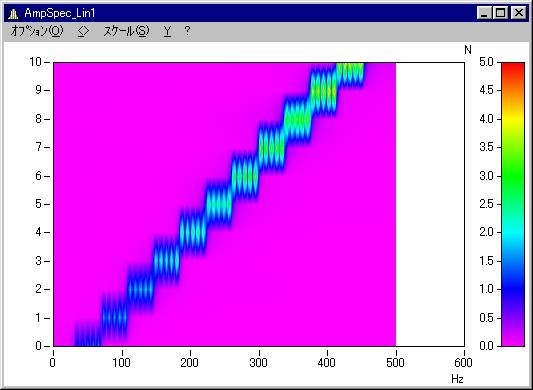
以下のサンプルシーケンスを利用して、参考結果として示します。
; サンプルデータの作成 _t = ramp(0,0.1, 30000) a1 = sqrt(2)*2*sin ( _t *(0.3*PI2)*(_t/400+1) )*(_t/1000+1) xdelta a1 0.001 ; パラメータ設定 AveragingType = 3 Reduction = 5 ; 関数 AmpSpec_Lin1 = AmpSpectrumRMS(a1,512,0,0,Reduction,AveragingType)
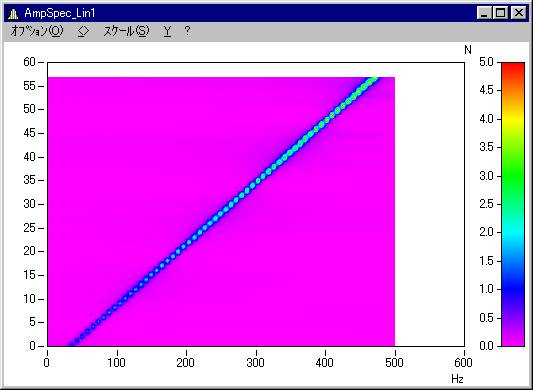
また、Reduction=5と指定した場合、5,10,15...番目のブロックが出力されます。
(Y軸の値はブロック数を示しています。5ブロック毎に出力されるため、57/5=11ブロックあります。)
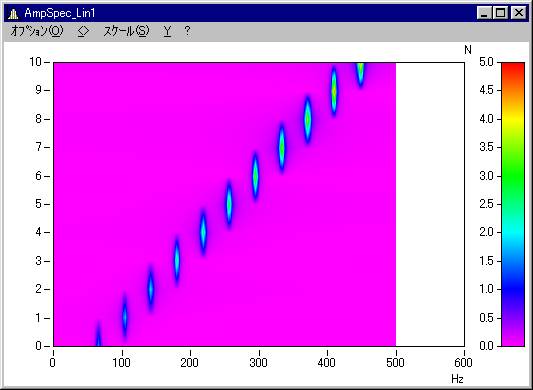
パラメータ:1
線形数値平均します。(平均化されるブロック数はパラメータ'Reduction'に依存します)
例えば、Reduction=5と指定した場合を示します。結果は、ブロック1~5までの平均値を1つの結果として、6~10、11~15...と続きます。
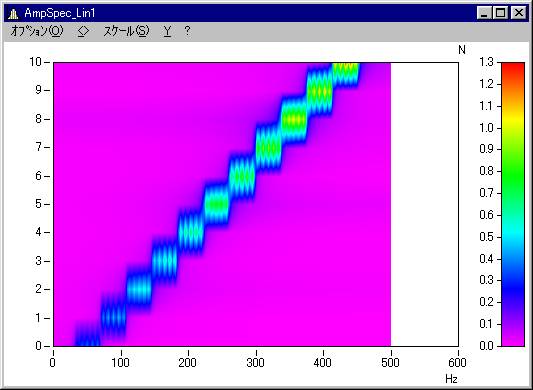
パラメータ:2
Reductionで指定した値により、指定ブロック毎に結果を出力します。
但し、Reductionの設定に拘わらず、計算結果は全てのブロックに対するピーク値を出力します。
下図はReduction=5を指定した例です。
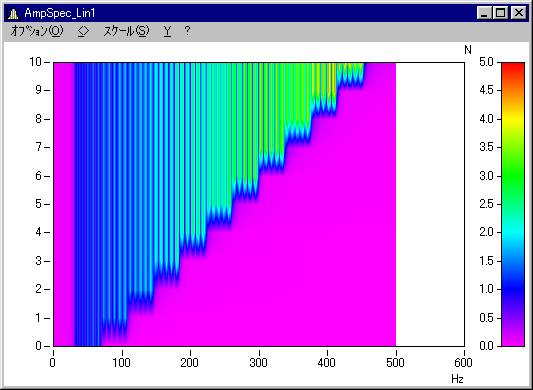
Reduction=1を指定すると、以下のようになります。
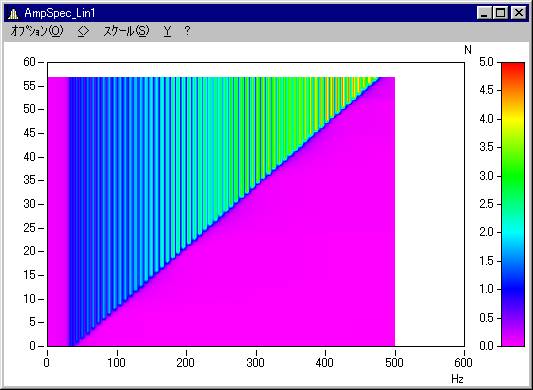
パラメータ:3
Reductionで設定された回数内でのスペクトラムのピーク値を求めます。
例えば、Reduction=5を指定すると、1番目の結果は1~5ブロックのピーク値を出力し、2番目の結果には6~10ブロックのピーク値を出力します。